
科目: 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:
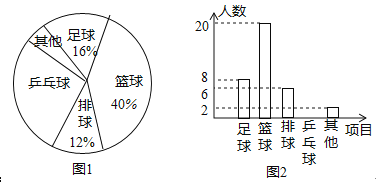
请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
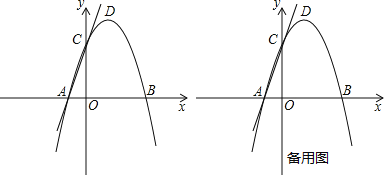
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】六一前夕某幼儿园园长到厂家选购A、B两种品牌的儿童服装每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍,求A、B两种品牌服装每套进价分别为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y1=k1x+b(k1≠0)与反比例函数![]() (k2≠0)的图象交于点A(4,1),B(n,-2)两点.
(k2≠0)的图象交于点A(4,1),B(n,-2)两点.
(1)求一次函数与反比例函数的解析式.
(2)求△AOB的面积.
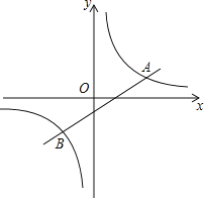
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在半⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是______.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是______.
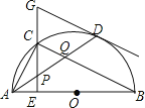
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y = x2+bx+c过点A (-1,2),且关于y轴对称,点C与点B(a,0)(a>1)关于原点对称,直线AC交抛物线于点D.
(1)求此抛物线的解析式;
(2)连接OA,BD,当OA//BD时,求a的值;
(3)若直线AC交抛物线![]() 于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.
于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,延长CO交AB于点D,记∠A=![]() ,∠ABC=β.
,∠ABC=β.
(1)求∠ADC的度数(用含α、β的式子表示);
(2)过点C作CE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F,CE,BF相交于点G,取![]() 中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.
中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商品的现在的售价为每件55元,每星期可卖出200件,如果每件商品的售价每上涨1元,则每星期少卖10件.已知商品进价为每件50元,进行涨价销售,每件售价是整数元,且不能高于70元.
(1)每件商品的售价定为多少元时,每星期可获得利润最大?最大利润是多少元?
(2)若在销售过程中每一件商品有m(m>1)元的其他费用,商家发现当售价每件不低于65元时,每星期的销售利润随定价的增大而减小,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的盒子里装有若干个黑、白两种颜色球,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)若从盒子里随机摸出一个球,则摸到白球的概率估计值为 (精确到0.1);
(2)若盒中黑球与白球若共有5个,小颖一次摸出两个球,请计算这两个球颜色不相同的概率,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com