
科目: 来源: 题型:
【题目】如图,直线x=t与反比例函数y=![]() ,y=﹣
,y=﹣![]() 的图象交于点A,B,直线y=2t与反比例y=
的图象交于点A,B,直线y=2t与反比例y=![]() ,y=﹣
,y=﹣![]() 的图象交于点C,D,其中常数t,k均大于0.点P,Q分别是x轴、y轴上任意点,若S△PCD=S1,S△ABQ=S2.则下列结论正确的是( )
的图象交于点C,D,其中常数t,k均大于0.点P,Q分别是x轴、y轴上任意点,若S△PCD=S1,S△ABQ=S2.则下列结论正确的是( )
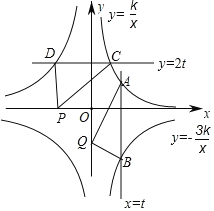
A.S1=2tB.S2=4kC.S1=2S2D.S1=S2
查看答案和解析>>
科目: 来源: 题型:
【题目】若矩形的一个短边与长边的比值为![]() ,(黄金分割数),我们把这样的矩形叫做黄金矩形
,(黄金分割数),我们把这样的矩形叫做黄金矩形
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD.
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
(3)归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)

查看答案和解析>>
科目: 来源: 题型:
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).

查看答案和解析>>
科目: 来源: 题型:
【题目】某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,有不重合的两个点Q(x1,y1)与P(x2,y2).若Q,P为某个直角三角形的两个锐角顶点,且该直角三角形的直角边均与x轴或y轴平行(或重合),则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“折距”,记做DPQ.特别地,当PQ与某条坐标轴平行(或重合)时,线段PQ的长即点Q与点P之间的“折距”.例如,在图1中,点P(1,-1),点Q(3,-2),此时点Q与点P之间的“折距”DPQ=3.
(1)①已知O为坐标原点,点A(3,-2),B(-1,0),则DAO=______,DBO=______.
②点C在直线y=-x+4上,请你求出DCO的最小值.
(2)点E是以原点O为圆心,1为半径的圆上的一个动点,点F是直线y=3x+6上以动点.请你直接写出点E与点F之间“折距”DEF的最小值.

查看答案和解析>>
科目: 来源: 题型:
【题目】正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线M:y=ax2-4ax+a-1(a≠0)与x轴交于A,B两点(点A在点B左侧),抛物线的顶点为D.
(1)抛物线M的对称轴是直线______;
(2)当AB=2时,求抛物线M的函数表达式以及顶点D的坐标;
(3)在(2)的条件下,直线l:y=kx+b(k≠0)经过抛物线的顶点D,直线y=n与抛物线M有两个公共点,它们的横坐标分别记为x1,x2,直线y=n与直线l的交点的横坐标记为x3(x3<4),若当-2≤n≤-1时,总有x1-x3<x3-x2<0,请结合函数的图象,直接写出k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,半圆O的直径AB=5cm,点M在AB上且AM=1cm,点P是半圆O上的动点,过点B作BQ⊥PM交PM(或PM的延长线)于点Q.设PM=xcm,BQ=ycm.(当点P与点A或点B重合时,y的值为0)小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
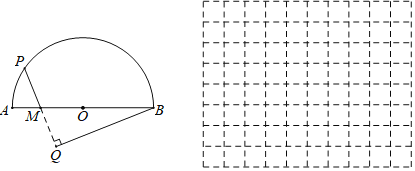
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 0 | 3.7 | ______ | 3.8 | 3.3 | 2.5 | ______ |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BQ与直径AB所夹的锐角为60°时,PM的长度约为______cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com