
科目: 来源: 题型:
【题目】 某学校为了了解九年级学生的体能情况,抽取了部分学生进行了体能测试,学生的测试成绩分四类:A:优秀;B:良好;C:合格;D不合格,将抽测学生的成绩绘制成如下两幅不完整的统计图,请根据统计图解答下列问题:
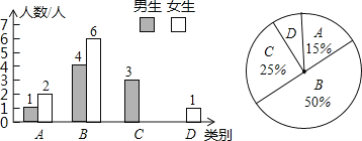
(1)求本次调查的学生总人数;
(2)成绩为C的女生有______人,成绩为D的男生有______人;
(3)扇形统计图中成绩为D的学生所对应的扇形的圆心角度数为______;
(4)补全条形统计图.
查看答案和解析>>
科目: 来源: 题型:
【题目】 如图,在△ABC中,∠ACB=90°,AC=BC过点C的射线CF交边AB于点F,AD⊥CF于点D,BE⊥CF于点E,AD=3,BE=1.
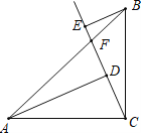
(1)求证:△ADC≌△CEB.
(2)求DE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】 如图,△ABC中,∠A=60°,AC>AB>2,点D,E分别在边AB,AC上,且BD=CE=2,连接DE,点M是DE的中点,点N是BC的中点,线段MN的长为______.
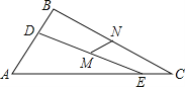
查看答案和解析>>
科目: 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目: 来源: 题型:
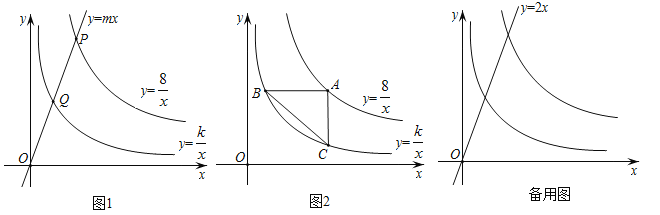
【题目】如图1,已知直线y=mx分别与双曲线y=![]() ,y=
,y=![]() (x>0)交于P,Q两点,且OP=2OQ.
(x>0)交于P,Q两点,且OP=2OQ.
(1)求k的值;
(2)如图2,若A是双曲线y=![]() 上的动点,AB∥x轴,AC∥y轴,分别交双曲线y=
上的动点,AB∥x轴,AC∥y轴,分别交双曲线y=![]() (x>0)于B,C两点,连接BC,设A点的横坐标为t.
(x>0)于B,C两点,连接BC,设A点的横坐标为t.
①分别写出A,B,C的坐标,并求△ABC的面积;
②当m=2时,D为直线y=2x上的一点,若以A,B,C,D为顶点的四边形是平行四边形,求A点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC是等边三角形,点P是平面内一点,且四边形PBCD为平行四边形,将线段CD绕点C逆时针旋转60°,得到线段CF
(1)如图1,当P为AC的中点时,求证:FC⊥PD.
(2)如图2,当P为△ABC内任一点时,连接PA、PF、AF,试判断△PAF的形状,并证明你的结论.
(3)当B、P、F三点共线且AB=![]() ,PB=3时,求PA的长.
,PB=3时,求PA的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】在数学课上,老师要求学生探究如下问题:
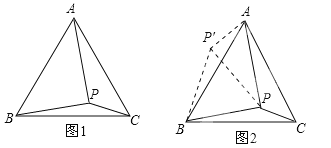
(1)如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,试求∠BPC的度数.李华同学一时没有思路,当他认真分析题目信息后,发现以PA、PB、PC的长为边构成的三角形是直角三角形,他突然有了正确的思路:如图2,将△BPC绕点B逆时针旋转60°,得到△BP′A,连接PP′,易得△P′PB是等边三角形,△PP′A是直角三角形.则∠BPC=_______°.
,PC=1,试求∠BPC的度数.李华同学一时没有思路,当他认真分析题目信息后,发现以PA、PB、PC的长为边构成的三角形是直角三角形,他突然有了正确的思路:如图2,将△BPC绕点B逆时针旋转60°,得到△BP′A,连接PP′,易得△P′PB是等边三角形,△PP′A是直角三角形.则∠BPC=_______°.
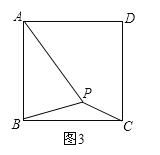
(2)如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1,试求∠BPC的度数.
,PC=1,试求∠BPC的度数.
(3)在图3中,若在正方形ABCD内有另一点Q,QA=a,QB=b,QC=c(a>b,a>c),试猜想a,b,c满足什么条件时,∠BQC的度数与第(2)问中∠BPC的度数相等,请直接写出结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】元旦期间,甲、乙两家商场都进行了促销活动,如何才能更好地衡量钏销对消费者受益程度的大小呢?某数学小组通过合作探究发现用优惠率p=![]() (其中k代表优惠金额,m代表顾客购买商品的总金额)可以很好地进行衡量,优惠率p越大,消费者受益程度越大;反之就越小.经统计,若顾客在甲、乙两家商场购买商品的总金额都为m(200≤m<400)元时,优惠率分别为P甲=
(其中k代表优惠金额,m代表顾客购买商品的总金额)可以很好地进行衡量,优惠率p越大,消费者受益程度越大;反之就越小.经统计,若顾客在甲、乙两家商场购买商品的总金额都为m(200≤m<400)元时,优惠率分别为P甲=![]() 与P乙=
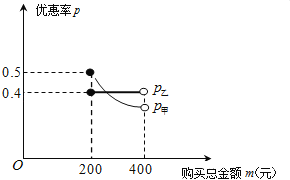
与P乙=![]() ,它们与m的关系图象如图所示,其中p甲与m成反比例函数关系,p乙保持定值.
,它们与m的关系图象如图所示,其中p甲与m成反比例函数关系,p乙保持定值.
(1)求出k甲的值,并用含m的代数式表示k乙.
(2)当购买总金额m(元)在200≤m<400的条件下时,指出甲、乙两家商场正在采取的促销方案分别是什么.
(3)品牌、质量、规格等都相同的基本种商品,在甲、乙两家商场的标价都是m(200≤m<400)元,你认为选择哪家商场购买该商品花钱少些?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,边长为4的正方形AOCD的顶点A、C分别在y轴和x轴上,点P的坐标为(2,0),以点P为圆心,OP的长为半径向正方形内部作一半圆,交线段DF于点F,线段DF的延长线交y轴于点E,DF=DC.
(1)求证:DF是半圆P的切线;
(2)求线段DF所在直线的解析式;

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线x=t(t>0)与双曲线y=![]() (k1>0)交于点A,与双曲线y=
(k1>0)交于点A,与双曲线y=![]() (k2<0)交于点B,连接OA,OB.
(k2<0)交于点B,连接OA,OB.
(1)当k1、k2分别为某一确定值时,随t值的增大,△AOB的面积_______(填增大、不变、或减小)
(2)当k1+k2=0,S△AOB=8时,求k1、k2的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com