
科目: 来源: 题型:
【题目】如图,在□ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是矩形;
(2)连接DE交BC于点F,连接AF,若CE=2,∠DAB=30°,求AF的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小东设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l上一点P.
![]()
求作:直线PQ,使得PQ⊥l.
作法:如图,
![]()
①在直线l上取一点A(不与点P重合),分别以点P,A为圆心,AP长为半径画弧,两弧在直线l的上方相交于点B;
②作射线AB,以点B为圆心,AP长为半径画弧,交AB的延长线于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接BP,
∵ = = =AP,
∴点A,P,Q在以点B为圆心,AP长为半径的圆上.
∴∠APQ=90°( ).(填写推理的依据)
即PQ⊥l.
查看答案和解析>>
科目: 来源: 题型:
【题目】世界上大部分国家都使用摄氏温度(℃),但美、英等国的天气预报仍然使用华氏温度(℉),两种计量之间有如下的对应表:
摄氏温度(℃) | 0 | 10 | 20 | 30 | 40 | 50 |
华氏温度(℉) | 32 | 50 | 68 | 86 | 104 | 122 |
由上表可以推断出,华氏0度对应的摄氏温度是_____℃,若某一温度时华氏温度的值与对应的摄氏温度的值相等,则此温度为_____℃.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
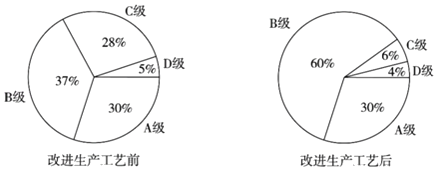
根据以上信息,下列推断合理的是( )
A.改进生产工艺后,A级产品的数量没有变化
B.改进生产工艺后,B级产品的数量增加了不到一倍
C.改进生产工艺后,C级产品的数量减少
D.改进生产工艺后,D级产品的数量减少
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0)两点,且交y轴交于点C.
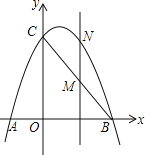
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
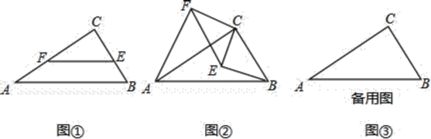
【题目】![]() 尝试探究:如图
尝试探究:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,E,F分别是BC,AC上的点,且
,E,F分别是BC,AC上的点,且![]() ,则
,则![]() ______;
______;
![]() 类比延伸:如图
类比延伸:如图![]() ,若将图
,若将图![]() 中的
中的![]() 绕点C顺时针旋转,则在旋转的过程中,
绕点C顺时针旋转,则在旋转的过程中,![]() 值是否发生变化?请仅就图
值是否发生变化?请仅就图![]() 的情形写出推理过程;
的情形写出推理过程;
![]() 拓展运用:若
拓展运用:若![]() ,
,![]() ,在旋转过程中,当B,E,F三点在同一直线上时,请直接写出此时线段AF的长.
,在旋转过程中,当B,E,F三点在同一直线上时,请直接写出此时线段AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和实数
和实数![]() ,给出如下定义:当
,给出如下定义:当![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆,称为点
为半径的圆,称为点![]() 的
的![]() 倍相关圆.
倍相关圆.
例如,在如图1中,点![]() 的1倍相关圆为以点
的1倍相关圆为以点![]() 为圆心,2为半径的圆.
为圆心,2为半径的圆.
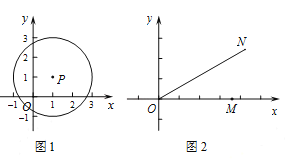
(1)在点![]() 中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
(2)如图2,若![]() 是
是![]() 轴正半轴上的动点,点
轴正半轴上的动点,点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,判断直线
,判断直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系,并证明.
倍相关圆的位置关系,并证明.
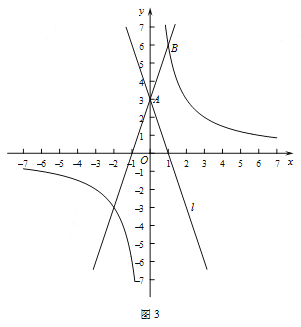
(3)如图3,已知点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的3倍相关圆的半径为________.
的3倍相关圆的半径为________.
②点![]() 在直线
在直线![]() 上,点
上,点![]() 的
的![]() 倍相关圆的半径为
倍相关圆的半径为![]() ,若点
,若点![]() 在运动过程中,以点
在运动过程中,以点![]() 为圆心,
为圆心,![]() 为半径的圆与反比例函数
为半径的圆与反比例函数![]() 的图象最多有两个公共点,直接写出
的图象最多有两个公共点,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com