
科目: 来源: 题型:
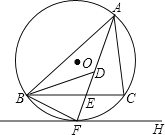
【题目】如图,⊙O是锐角△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.下列结论:①AF平分∠BAC;②点F为△BDC的外心;③![]() ;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是_____(把你认为正确结论的序号都填上).
;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是_____(把你认为正确结论的序号都填上).
查看答案和解析>>
科目: 来源: 题型:
【题目】某品牌的饮水机接通电源后就进入自动程序:开机加热到水温 100℃, 停止加热,水温开始下降,此时水温 y(℃)与开机后用时 x(min)成反比 例关系,直至水温降至 30℃,饮水机关机.饮水机关机后即刻自动开机,重 复上述自动程序.若在水温为 30℃时,接通电源后,水温 y(℃)和时间 x(min)的关系如图所示,水温从 100℃降到 35℃所用的时间是________min.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.

(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知实数a,c满足![]() ,2a+c﹣ac+2>0,二次函数y=ax2+bx+9a经过点B(4,n)、A(2,n),且当1≤x≤2时,y=ax2+bx+9a的最大值与最小值之差是9,求a的值.
,2a+c﹣ac+2>0,二次函数y=ax2+bx+9a经过点B(4,n)、A(2,n),且当1≤x≤2时,y=ax2+bx+9a的最大值与最小值之差是9,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=5,AD=3.点E是CD上的动点,以AE为直径的⊙O与AB交于点F,过点F作FG⊥BE于点G.
(1)若E是CD的中点时,证明:FG是⊙O的切线
(2)试探究:BE能否与⊙O相切?若能,求出此时DE的长;若不能,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
小红遇到这样一个问题:如图1,在四边形ABCD中,∠A=∠C=90°,∠D=60°,AB=![]() ,BC=
,BC=![]() ,求AD的长.
,求AD的长.
小红发现,延长AB与DC相交于点E,通过构造Rt△ADE,经过推理和计算能够使问题得到解决(如图2).
请回答:AD的长为 .
参考小红思考问题的方法,解决问题:
如图3,在四边形ABCD中,tanA=![]() ,∠B=∠C=135°,AB=9,CD=3,求BC和AD的长.
,∠B=∠C=135°,AB=9,CD=3,求BC和AD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,O为原点,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.过点P作PB∥x轴,与直线AQ交于点B,如果AP⊥BO,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】(9分)为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表:
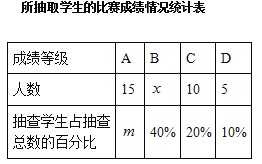
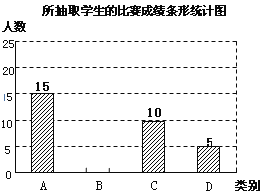
根据图表的信息,回答下列问题:
(1)本次抽查的学生共有 名;
(2)表中![]() 和
和![]() 所表示的数分别为:
所表示的数分别为:![]() ,
,![]() ,并在图中补全条形统计图;
,并在图中补全条形统计图;
(3)若该校共有![]() 名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?
名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?
查看答案和解析>>
科目: 来源: 题型:
【题目】10个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实地告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报2的人心里想的数是____.

查看答案和解析>>
科目: 来源: 题型:
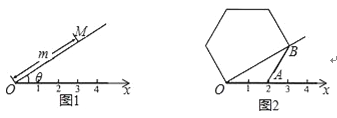
【题目】规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
A.(![]() ,30°) B.(60°,
,30°) B.(60°,![]() )
)
C.(30°,4) D.(30°,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com