
科目: 来源: 题型:
【题目】下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:直线![]() 及直线
及直线![]() 外一点P.
外一点P.

求作:直线![]() ,使
,使![]() .
.
作法:如图,

①在直线![]() 上取一点O,以点O为圆心,
上取一点O,以点O为圆心,![]() 长为半径画半圆,交直线
长为半径画半圆,交直线![]() 于
于![]() 两点;
两点;
②连接![]() ,以B为圆心,
,以B为圆心,![]() 长为半径画弧,交半圆于点Q;
长为半径画弧,交半圆于点Q;
③作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小明设计的尺规作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明
证明:连接![]() ,
,
∵![]() ,
,
∴![]() __________.
__________.
∴![]() (______________)(填推理的依据).
(______________)(填推理的依据).
∴![]() (_____________)(填推理的依据).
(_____________)(填推理的依据).
查看答案和解析>>
科目: 来源: 题型:
【题目】电影公司随机收集了2000部电影的有关数据,经分类整理得到如表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
好评率 |
|
|
|
|
|
|
注:好评率是指一类电影中获得好评的部数与该类电影的部数的比值.
![]() 如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
![]() 电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化
电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化![]() 假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加
假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加![]() ,哪类电影的好评率减少
,哪类电影的好评率减少![]() ,可使改变投资策略后总的好评率达到最大?
,可使改变投资策略后总的好评率达到最大?
答:______.
查看答案和解析>>
科目: 来源: 题型:
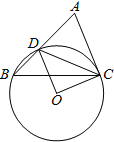
【题目】已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.如果∠ACB=75°,圆O的半径为2,则BD的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,荧光屏上的甲、乙两个光斑(可看作点)分别从相距8cm的A,B两点同时开始沿线段AB运动,运动工程中甲光斑与点A的距离S1(cm)与时间t(s)的函数关系图象如图2,乙光斑与点B的距离S2(cm)与时间t(s)的函数关系图象如图3,已知甲光斑全程的平均速度为1.5cm/s,且两图象中△P1O1Q1≌P2Q2O2,下列叙述正确的是( )

A. 甲光斑从点A到点B的运动速度是从点B到点A的运动速度的4倍
B. 乙光斑从点A到B的运动速度小于1.5cm/s
C. 甲乙两光斑全程的平均速度一样
D. 甲乙两光斑在运动过程中共相遇3次
查看答案和解析>>
科目: 来源: 题型:
【题目】下面的统计图反映了我国出租车(巡游出租车和网约出租车)客运量结构变化.
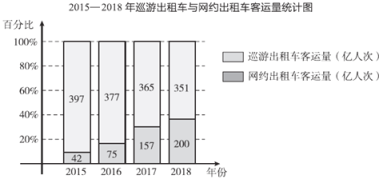
(以上数据摘自《中国共享经济发展年度报告(2019)》)
根据统计图提供的信息,下列推断合理的是( )
A.2018年与2017年相比,我国网约出租车客运量增加了20%以上
B.2018年,我国巡游出租车客运量占出租车客运总量的比例不足60%
C.2015年至2018年,我国出租车客运的总量一直未发生变化
D.2015年至2018年,我国巡游出租车客运量占出租车客运总量的比例逐年增加
查看答案和解析>>
科目: 来源: 题型:
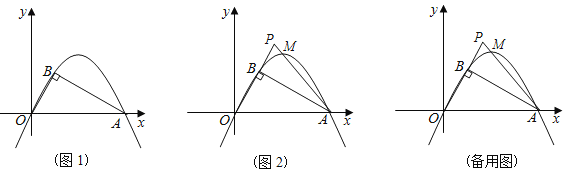
【题目】如图1,抛物线y=ax2+bx经过原点O和点A(12,0),在B在抛物线上,已知OB⊥BA,且∠A=30°.
(1)求此抛物线的解析式.
(2)如图2,点P为OB延长线上一点,若连接AP交抛物线于点M,设点P的横坐标为t,点M的横坐标为m,试用含有t的代数式表示m,不要求写取值范围.
(3)在(2)的条件下,过点O作OW⊥AP于W,并交线段AB于点G,过点W的直线交OP延长线于点N,交x轴于点K,若∠WKA=2∠OAP,且NK=11,求点M的横坐标及WG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,四边形ABGC内接于⊙O,GA平分∠BGC.
(1)求证:AB=AC;
(2)如图2,过点A作AD∥BG交CG于点D,连接BD交线段AG于点W,若∠BAG+∠CAD=∠AWB,求证:BD=BG;
(3)在(2)的条件下,若CD=5,BD=16,求WG的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】澜鑫商场为“双十一购物节”请甲乙两个广告公司布置展厅,已知乙单独完成此项任务的天数是甲单独完成此任务天数的2倍.若两公司合作4天,再由甲公司单独做3天就可以完成任务.
(1)甲公司与乙公司单独完成这项任务各需多少天?
(2)甲公司每天所需费用为5万元,乙公司每天所需费用为2万元,要使这项工作的总费用不超过40万元,则甲公司至多工作多少天?
查看答案和解析>>
科目: 来源: 题型:
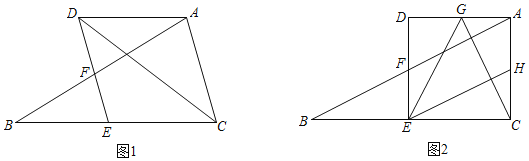
【题目】在△ABC中,过A作BC的平行线,交∠ACB的平分线于点D,点E是BC上一点,连接DE,交AB于点F,∠DEB+∠CAD=180°.
(1)如图1,求证:四边形ACED是菱形;
(2)如图2,G是AD的中点,H是AC边中点,连接CG、EG、EH,若∠ACB=90°,BC=2AC,在不添加任何辅助线的情况下,请直接写出图中与△CEH全等的三角形(不含△CEH本身).
查看答案和解析>>
科目: 来源: 题型:
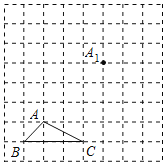
【题目】如图,正方形网格中,小正方形的边长为1.△ABC的顶点都在格点上.
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1逆时针旋转90°,在网格中画出旋转后的△A1B2C2;
(3)在(2)的条件下,直接写出点C1至点C2的经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com