
科目: 来源: 题型:
【题目】菱形ABCD中,点P为CD上一点,连接BP.
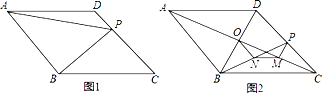
(1)如图1,若BP⊥CD,菱形ABCD边长为10,PD=4,连接AP,求AP的长.
(2)如图2,连接对角线AC、BD相交于点O,点N为BP的中点,过P作PM⊥AC于M,连接ON、MN.试判断△MON的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
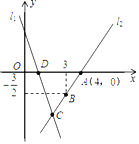
(1)求直线l2的解析表达式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请求出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是某小区入口实景图,图2是该入口抽象成的平面示意图,已知入口BC宽3.9米,门卫室外墙上的O点处装有一盏灯,点O与地面BC的距离为3.3米,灯臂OM长1.2米,(灯罩长度忽略不计),∠AOM=60°.

(1)求点M到地面的距离,
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车能否从该入口安全通过?如果能安全通过,请直接写出货车离门卫室外墙AB的最小距离(精确到0.01米);如果不能安全通过,请说明理由.(参考数据:![]() 1.73)
1.73)
查看答案和解析>>
科目: 来源: 题型:
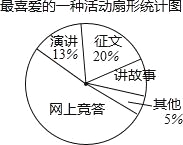
【题目】近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
人数 | 60 | 30 | 39 | a | b |
(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,把平面内一条数轴x绕点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:已知点P是平面斜坐标系中任意一点,过点P作y轴的平行线交x轴于点A,过点P作x轴的平行线交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标.在平面斜坐标系中,若θ=45°,点P的斜坐标为(1,2![]() ),点G的斜坐标为(7,﹣2
),点G的斜坐标为(7,﹣2![]() ),连接PG,则线段PG的长度是_____.
),连接PG,则线段PG的长度是_____.

查看答案和解析>>
科目: 来源: 题型:
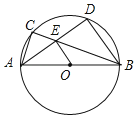
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D是![]() 的中点,AD交BC于点E,若CE=
的中点,AD交BC于点E,若CE=![]() ,BE=
,BE=![]() ,以下结论中:①sin∠ABC=
,以下结论中:①sin∠ABC=![]() ;②AD=
;②AD=![]() ,③S⊙O=
,③S⊙O=![]() π;④OE∥BD.其中正确的共有( )个.
π;④OE∥BD.其中正确的共有( )个.
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在ABCD中,AB=3,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF的周长为( )
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF的周长为( )
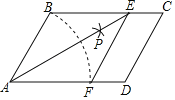
A.12B.14C.16D.18
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某商品标牌的示意图,⊙O与等边△ABC的边BC相切于点C,且⊙O的直径与△ABC的高相等,已知等边△ABC边长为4,设⊙O与AC相交于点E,则AE的长为( )
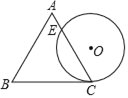
A.![]() B.1C.
B.1C.![]() ﹣1D.
﹣1D.![]()
查看答案和解析>>
科目: 来源: 题型:
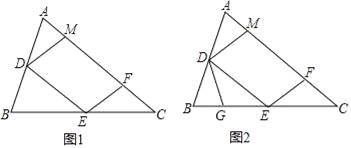
【题目】如图1,在锐角△ABC中,D、E分别是AB、BC的中点,点F在AC上,且满足∠AFE=∠A,DM∥EF交AC于点M.
(1)证明:DM=DA;
(2)如图2,点G在BE上,且∠BDG=∠C,求证:△DEG∽△ECF;
(3)在图2中,取CE上一点H,使得∠CFH=∠B,若BG=3,求EH的长.
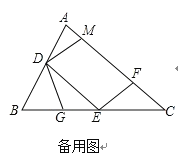
查看答案和解析>>
科目: 来源: 题型:
【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com