
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“距离”,记作![]() 特别地,若图形M,N有公共点,规定
特别地,若图形M,N有公共点,规定![]() .
.
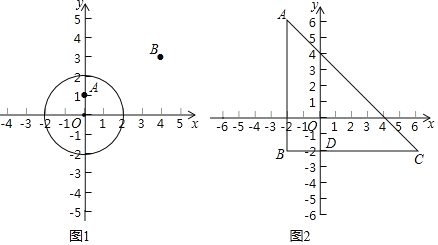
![]() 如图1,
如图1,![]() 的半径为2,
的半径为2,
![]() 点
点![]() ,
,![]() ,则
,则![]() ______,
______,![]() ______.
______.
![]() 已知直线l:
已知直线l:![]() 与
与![]() 的“距离”
的“距离”![]() ,求b的值.
,求b的值.
![]() 已知点
已知点![]() ,
,![]() ,
,![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() 若
若![]() ,请直接写出m的取值范围______.
,请直接写出m的取值范围______.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数![]() 的图象交x轴于A(-1, 0),B(4, 0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC.设运动的时间为t秒.
的图象交x轴于A(-1, 0),B(4, 0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC.设运动的时间为t秒.
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接BD,当![]() 时,求△DNB的面积;
时,求△DNB的面积;
(3)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,直接写出此时点D的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂用![]() 天时间生产一款新型节能产品,每天生产的该产品被某网店以每件
天时间生产一款新型节能产品,每天生产的该产品被某网店以每件![]() 元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第
元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第![]() 天的生产成本
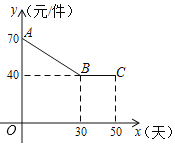
天的生产成本![]() (元/件)与
(元/件)与![]() (天)之间的关系如图所示,第
(天)之间的关系如图所示,第![]() 天该产品的生产量
天该产品的生产量![]() (件)与
(件)与![]() (天)满足关系式
(天)满足关系式![]()
![]() 第
第![]() 天,该厂生产该产品的利润是 元;
天,该厂生产该产品的利润是 元;
![]() 设第
设第![]() 天该厂生产该产品的利润为
天该厂生产该产品的利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在生产该产品的过程中,当天利润不低于![]() 元的共有多少天?
元的共有多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目: 来源: 题型:
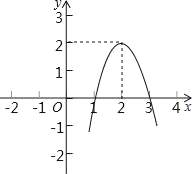
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
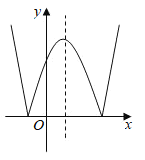
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
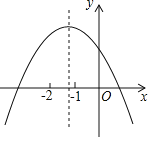
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点P为∠MAN边AM上一动点,⊙P切AN于点C,与AM交于点D(点D在点P的右侧),作DF⊥AN于F,交⊙O于点E.
(1)连接PE,求证:PC平分∠APE;
(2)若DE=2EF,求∠A的度数;
(3)点B为射线AN上一点,且AB=8,射线BD交⊙P于点Q,sin∠A=![]() .在P点运动过程中,是否存在某个位置,使得△DQE为等腰三角形?若存在,求出此时AP的长;若不存在,请说明理由.
.在P点运动过程中,是否存在某个位置,使得△DQE为等腰三角形?若存在,求出此时AP的长;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com