
科目: 来源: 题型:
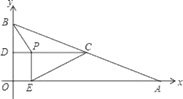
【题目】在平面直角坐标系中,已知点A、B的坐标分别为(10,0)、(0,4),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C以每秒1个单位匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P运动的时间为_____秒.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知⊙C的半径为2,圆外一点O满足OC=3.5,点P为⊙C上一动点,经过点O的直线l上有两点A、B,且OA=OB,∠APB=90°,l不经过点C,则AB的最小值为( )
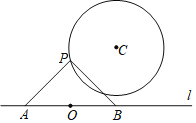
A. 2 B. 2.5 C. 3 D. 3.5
查看答案和解析>>
科目: 来源: 题型:
【题目】下列判断正确的是( )
A. “任意选择某一电视频道,它正在播放动画片”是必然事件
B. 某运动员投一次篮,投中的概率为0.8,则该运动员投5次篮,一定有4次投中
C. 任意抛掷一枚均匀的硬币,反面朝上的概率为![]()
D. 布袋里有3个白球,1个黑球.任意取出1个球,恰好是黑球的概率是![]()
查看答案和解析>>
科目: 来源: 题型:
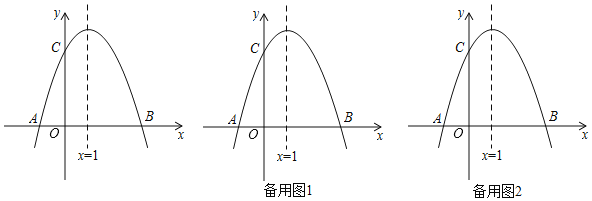
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于A、B两点,AB=4,交y轴于点C,对称轴是直线x=1.
(1)求抛物线的解析式及点C的坐标;
(2)连接BC,E是线段OC上一点,E关于直线x=1的对称点F正好落在BC上,求点F的坐标;
(3)动点M从点O出发,以每秒2个单位长度的速度向点B运动,过M作x轴的垂线交抛物线于点N,交线段BC于点Q.设运动时间为t(t>0)秒.
①若△AOC与△BMN相似,请直接写出t的值;
②△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了加快“智慧校园”建设,某市准备为试点学校采购一批![]() 、
、![]() 两种型号的一体机,经过市场调查发现,今年每套
两种型号的一体机,经过市场调查发现,今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机.
型一体机.
(1)求今年每套![]() 型、
型、![]() 型一体机的价格各是多少万元
型一体机的价格各是多少万元
(2)该市明年计划采购![]() 型、
型、![]() 型一体机1100套,考虑物价因素,预计明年每套
型一体机1100套,考虑物价因素,预计明年每套![]() 型一体机的价格比今年上涨25%,每套
型一体机的价格比今年上涨25%,每套![]() 型一体机的价格不变,若购买
型一体机的价格不变,若购买![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买![]() 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
查看答案和解析>>
科目: 来源: 题型:
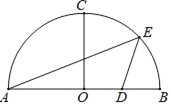
【题目】如图,AB是半圆O的直径,半径OC⊥AB,OB=4,D是OB的中点,点E是弧BC上的动点,连接AE, DE.
(1)当点E是弧BC的中点时,求△ADE的面积;
(2)若tan∠AED=![]() ,求AE的长;
,求AE的长;
(3)点F是半径OC上一动点,设点E到直线OC的距离为m,
①当△DEF是等腰直角三角形时,求m的值;
②延长DF交半圆弧于点G,若弧AG=弧EG,AG∥DE,直接写出DE的长 .
查看答案和解析>>
科目: 来源: 题型:
【题目】现有一块矩形地皮,计划共分九个区域区域甲、乙是两个矩形主体建筑,区域丙为梯形停车场,区城①-④是四块三角形绿化区,△AEL和△CIJ为综合办公区(如图所示).∠HEL=∠ELI=90°,MN//BC.AD=220米,AL=40米,AE=IC=30米.
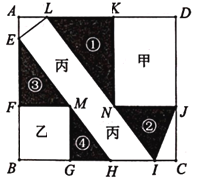
(1)求HI的长
(2)若BG=KD,求主体建筑甲和乙的面积和.
(3)设LK=3x米,绿化区②的面积为S平方米.若要求绿化区②与④的面积之差不少于1200平方米,求S关于x的函数表达式.并求出S的最小值
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=-x2+4x-1与y轴交于点C,CD∥x轴交抛物线于另一点D,AB∥x轴交抛物线于点A,B,点A在点B的左侧,且两点均在第一象限,BH⊥CD于点H.设点A的横坐标为m.
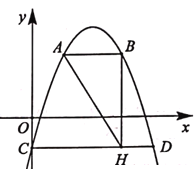
(1)当m=1时,求AB的长.
(2)若AH=![]() (CH-DH),求m的值.
(CH-DH),求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com