
科目: 来源: 题型:
【题目】在信息技术飞速发展的今天,智能手机的使用呈现出低龄化的趋势,中小学生使用智能手机成为十分普遍的现象,但智能手机给生活带来便利的同时,也对中小学生的身心发展带来一些不利影响,比如手机屏幕对视力的伤害、关注各种“垃圾新闻”对时间的浪费、沉迷手机游戏缺少运动、人际交往等等,这些现象引起了家长、学校、社会的广泛关注.对此,成都某中学学生会发出了“中小学生使用非智能手机”的倡议,鼓励同学们全面发展,追逐梦想,把更多时间用在将来能够成就自我的地方.据统计,今年9月该中学使用非智能手机的同学有128人,倡议发出后,11月使用非智能手机的同学上升到了200人.
(1)若从9月到11月使用非智能手机的同学平均增长率相同,那么按此增长率增长到12月份该校使用非智能手机的同学将有多少人?
(2)某于机制造商发现当下市场上售卖的非智能手机大多品质不佳、外观设计成就,难以满足市场的需要,所以该厂决定投入12万元全部用于生产![]() 型、
型、![]() 型两款精美的“学生专用手机”投入市场,一部
型两款精美的“学生专用手机”投入市场,一部![]() 型手机生产成本为400元,售价为600元;一部
型手机生产成本为400元,售价为600元;一部![]() 型手机生产成本为600元,售价为930元,该厂计划生产
型手机生产成本为600元,售价为930元,该厂计划生产![]() 型手机的数量不少于
型手机的数量不少于![]() 型手机数量的2倍,但不超过
型手机数量的2倍,但不超过![]() 型手机数量的2.3倍,求生产这批手机并全部售卖后可获得的最大利润.
型手机数量的2.3倍,求生产这批手机并全部售卖后可获得的最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与轴负半轴交于点
的左侧),与轴负半轴交于点![]() ,若
,若![]() .
.
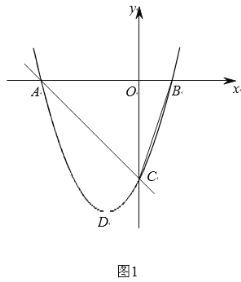
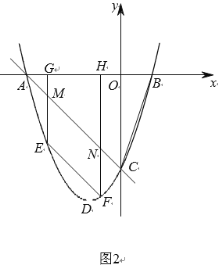
(1)求抛物线的解析式;
(2)如图2,![]() 是第三象限内抛物线上的动点,过点
是第三象限内抛物线上的动点,过点![]() 交抛物线于点
交抛物线于点![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,当四边形
,当四边形![]() 的周长最大值时,求点
的周长最大值时,求点![]() 的横坐标;
的横坐标;
(3)在![]() 轴下方的抛物线上是否存在一点
轴下方的抛物线上是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形被对角线分成面积相等的两部分.如果存在,求点
为顶点的四边形被对角线分成面积相等的两部分.如果存在,求点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们可以用![]() 表示
表示![]() 为自变量的函数,如一次函数
为自变量的函数,如一次函数![]() ,可表示
,可表示![]() ,
,![]() ,
,![]() .
.
(1)已知二次函数![]() ;
;
①求证:不论![]() 为何值,此函数图像与
为何值,此函数图像与![]() 轴总有两个交点;
轴总有两个交点;
②若![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)已知函数![]() ,
,![]() ,若实数
,若实数![]() 、
、![]() 使得
使得![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】熊组长准备为我们年级投资1万元围一个矩形的运动场地(如图),其中一边靠墙,另外三边选用不同材料建造且三边的总长为![]() ,墙长
,墙长![]() ,平行于墙的边的费用为200元/
,平行于墙的边的费用为200元/![]() ,垂直于墙的边的费用150元/
,垂直于墙的边的费用150元/![]() ,设平行与墙的边长为
,设平行与墙的边长为![]() .
.
(1)若运动场地面积为![]() ,求
,求![]() 的值;
的值;
(2)当运动场地的面积最大时是否会超了预算.

查看答案和解析>>
科目: 来源: 题型:
【题目】为监控某条生产线上产品的质量,检测员每隔相同时间抽取一件产品,并测量其尺寸(![]() ),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
尺寸 | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 |
| 9.03 | 9.04 | 9.06 | 9.07 | 9.08 |
|
按照生产标准,产品等级规定如下:
尺寸(单位: | 产品等次 |
| 特等品 |
| 优等品 |
| 合格品 |
| 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格个数时,将优等品(含特等品)算在内,
(1)已知此次抽检的合格率为![]() ,请判断编号为15的产品是否为合格品,并说明理由;
,请判断编号为15的产品是否为合格品,并说明理由;
(2)已知此次及抽检出的优等品尺寸的中位数为![]() .
.
①![]() __________;
__________;
②将这些优等品分成两组,一组尺寸大于![]() ,另一种尺寸不大于
,另一种尺寸不大于![]() ,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】(中考·安徽)如图,已知反比例函数y=![]() 与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).
与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).

(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)是反比例函数y=![]() 的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于原点对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出线段OB旋转到OB2扫过图形的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+2nx+c的图象过坐标原点.
(1)若a=-1.
①当函数自变量的取值范围是-1≤x≤2,且n≥2时,该函数的最大值是8,求n的值;
②当函数自变量的取值范围是![]() 时,设函数图象在变化过程中最高点的纵坐标为m,求m与n的函数关系式,并写出n的取值范围;
时,设函数图象在变化过程中最高点的纵坐标为m,求m与n的函数关系式,并写出n的取值范围;
(2)若二次函数的图象还过点A(-2,0),横、纵坐标都是整数的点叫做整点.已知点![]() ,二次函数图象与直线AB围城的区域(不含边界)为T,若区域T内恰有两个整点,直接写出a的取值范围.
,二次函数图象与直线AB围城的区域(不含边界)为T,若区域T内恰有两个整点,直接写出a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com