
科目: 来源: 题型:
【题目】暑假期间,为激发同学们的学习热情,王华所在的学校组织全校三好学生分别到A,B,C,D四所全国重点学校参观(每个学生只能去一处),王华很高兴她也能够前往,学校按定额购买了前往四地的车票.如图是未制作完成的车票种类和数量的条形统计图和扇形统计图.请根据以上信息回答:

(1)本次参加参观的学生有 人,将条形统计图补充完整;
(2)若学校采用随机抽取的方式分发车票,每人一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么王华抽到去B地的概率是多少?
(3)已知A,B,C三地车票的价格如下表,去D地花费的车票总款数占全部车票总款数的![]() ,试求D地每张车票的价格.
,试求D地每张车票的价格.
地点 | 票价(元/张) |
A | 60 |
B | 80 |
C | 50 |
查看答案和解析>>
科目: 来源: 题型:
【题目】在求两位数的平方时,可以用完全平方式及“列竖式”的方法进行速算,求解过程如下.
例如:求322.
解:因为(3x+2y)2=9x2+4y2+12xy,将上式中等号右边的系数填入下面的表格中可得:
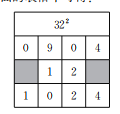
所以322=1024.
(1)下面是嘉嘉仿照例题求892的一部分过程,请你帮他填全表格及最后结果;
解:因为(8x+9y)2=64x2+81y2+144xy,将上式中等号右边的系数填入下面的表格中可得:
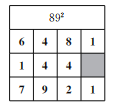
所以892= ;
(2)仿照例题,速算672;
(3)琪琪用“列竖式”的方法计算一个两位数的平方,部分过程如图所示.若这个两位数的个位数字为a,则这个两位数为 (用含a的代数式表示).

查看答案和解析>>
科目: 来源: 题型:
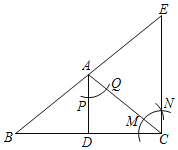
【题目】如图,在△ABC中,AD为边BC上的中线,且AD平分∠BAC.嘉淇同学先是以A为圆心,任意长为半径画弧,交AD于点P,交AC于点Q,然后以点C为圆心,AP长为半径画弧,交AC于点M,再以M为圆心,PQ长为半径画弧,交前弧于点N,作射线CN,交BA的延长线于点E.
(1)通过嘉淇的作图方法判断AD与CE的位置关系是 ,数量关系是 ;
(2)求证:AB=AC;
(3)若BC=24,CE=10,求△ABC的内心到BC的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在某条公路上有A,B,C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,又以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图2所示.
(1)当汽车在A,B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)当汽车的行驶路程为360千米时,求此时的行驶时间x的值;
(3)若汽车在某一段路程内行驶了90千米用时50分钟,求行驶完这段路程时x的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,O是AD的中点,以O为圆心在AD的下方作半径为3的半圆O,交AD于E、F.
思考:连接BD,交半圆O于G、H,求GH的长;
探究:将线段AF连带半圆O绕点A顺时针旋转,得到半圆O′,设其直径为E'F′,旋转角为α(0<α<180°).
(1)设F′到AD的距离为m,当m>![]() 时,求α的取值范围;
时,求α的取值范围;
(2)若半圆O′与线段AB、BC相切时,设切点为R,求![]() 的长.
的长.
(sin49°=![]() ,cos41°=
,cos41°=![]() ,tan37°=
,tan37°=![]() ,结果保留π)
,结果保留π)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,ΔABC中,AB=AC,∠A=40O,延长AC到D,使CD=BC,点P是ΔABD的内心,则∠BPC=

A. 105° B. 110° C. 130° D. 145°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在A、B 两地之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A,B两地同时开工,若干天后公路准确接通,若公路AB长8千米,另一条公路BC长是6千米,且BC的走向是北偏西42°,则A地到公路BC的距离是( )

A. 6千米 B. 8千米 C. 10千米 D. 14千米
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点C是∠AOB的平分线上一点,点P、P′分别在边OA、OB上.如果要得到 OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能的结果的序号为( )

①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
A.①②B.④③C.①④③D.①②④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 的三个顶点,与
的三个顶点,与![]() 轴相交于
轴相交于![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.

(1)求该抛物线的函数解析式;
(2)点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴,
轴,![]() 轴, 垂足分别为点
轴, 垂足分别为点![]() ,
,![]() ,当四边形
,当四边形![]() 为正方形时,求出点
为正方形时,求出点![]() 的坐标;
的坐标;
(3)将(2) 中的正方形![]() 沿
沿![]() 向右平移,记平移中的正方形
向右平移,记平移中的正方形![]() 为正方形
为正方形![]() ,当点
,当点![]() 和点
和点![]() 重合时停止运动, 设平移的距离为
重合时停止运动, 设平移的距离为![]() ,正方形的边
,正方形的边![]() 与
与![]() 交于点
交于点![]() ,
,![]() 所在的直线与
所在的直线与![]() 交于点
交于点![]() , 连接
, 连接![]() ,是否存在这样的
,是否存在这样的![]() ,使
,使![]() 是等腰三角形?若存在,求
是等腰三角形?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com