
科目: 来源: 题型:
【题目】关于二次函数y=x2+2x+3的图象有以下说法:其中正确的个数是( )
①它开口向下;②它的对称轴是过点(﹣1,3)且平行于y轴的直线;③它与x轴没有公共点;④它与y轴的交点坐标为(3,0).
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】对于某一函数给出如下定义:对于任意实数![]() ,当自变量
,当自变量![]() 时,函数
时,函数![]() 关于
关于![]() 的函数图象为
的函数图象为![]() ,将
,将![]() 沿直线
沿直线![]() 翻折后得到的函数图象为
翻折后得到的函数图象为![]() ,函数
,函数![]() 的图象由
的图象由![]() 和
和![]() 两部分共同组成,则函数
两部分共同组成,则函数![]() 为原函数的“对折函数”,如函数
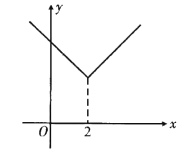
为原函数的“对折函数”,如函数![]() (
(![]() )的对折函数为
)的对折函数为![]() .
.
(1)求函数![]() (
(![]() )的对折函数;
)的对折函数;
(2)若点![]() 在函数
在函数![]() (
(![]() )的对折函数的图象上,求
)的对折函数的图象上,求![]() 的值;
的值;
(3)当函数![]() (
(![]() )的对折函数与
)的对折函数与![]() 轴有不同的交点个数时,直接写出
轴有不同的交点个数时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴正半轴交于
轴正半轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() .
.
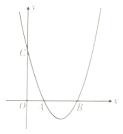
(1)利用直尺和圆规,作出抛物线![]() 的对称轴(尺规作图,保留作图痕迹,不写作法);
的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若![]() 是等腰直角三角形,且其腰长为3,求
是等腰直角三角形,且其腰长为3,求![]() 的值;
的值;
(3)在(2)的条件下,点![]() 为抛物线对称轴上的一点,则
为抛物线对称轴上的一点,则![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了46米木栏.
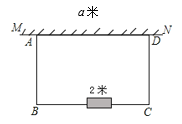
(1)若a=26,所围成的矩形菜园的面积为280平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】阿波罗尼奥斯(Apollonius of Perga,约公元前262-190年),古希腊数学家,与欧几里得,阿基米德齐名,他的著作《圆锥曲线论》是古代世界光辉的科学成果.
材料:《圆锥曲线论》里面对抛物线的定义:平面内一个动点到一个定点与一条定直线的距离之比等于1,或者说:平面内一动点到一定点与一条直线的距离相等的轨迹就是抛物线.
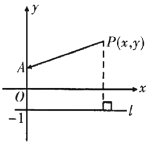
问题:已知点![]() ,
,![]() ,直线
,直线![]() ,连接
,连接![]() ,若点
,若点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长相等,请求出
的长相等,请求出![]() 与
与![]() 的关系式.
的关系式.
解:如图,∵![]() ,
,![]() ,
,
∴![]()
∵![]() ,直线
,直线![]() ,
,
∴点![]() 到直线
到直线![]() 的距离为
的距离为![]()
∵点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长相等,
的长相等,
∴![]() ,
,
平方化简得,![]() .
.
若将上述问题中![]() 点坐标改为
点坐标改为![]() ,直线
,直线![]() 变为
变为![]() ,按照问题解题思路,试求出
,按照问题解题思路,试求出![]() 与
与![]() 的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
查看答案和解析>>
科目: 来源: 题型:
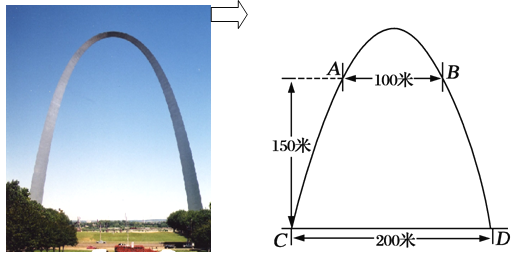
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;

查看答案和解析>>
科目: 来源: 题型:
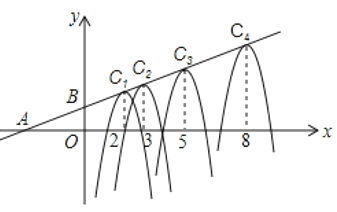
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,形状相同的抛物线
,形状相同的抛物线![]() 的顶点在直线
的顶点在直线![]() 上,其对称轴与
上,其对称轴与![]() 轴的交点的横坐标依次为2,3,5,18,13,…,根据上述规律,抛物线
轴的交点的横坐标依次为2,3,5,18,13,…,根据上述规律,抛物线![]() 的顶点坐标为_________.
的顶点坐标为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com