
科目: 来源: 题型:
【题目】我们约定,在平面直角坐标系中两条抛物线有且只有一个交点时,我们称这两条抛物线为“郡园牵手抛物线”,这个交点为“郡园点”.例如:抛物线![]() 与
与![]() 是“郡园牵手抛物线”,“郡园点”为
是“郡园牵手抛物线”,“郡园点”为![]() .
.
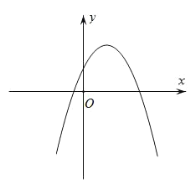
(1)如图,若抛物线![]() 与
与![]() 为“郡园牵手抛物线”,求
为“郡园牵手抛物线”,求![]() 的值;
的值;
(2)在(1)的条件下,若点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上的动点,过
上的动点,过![]() 作
作![]() 轴,
轴,![]() 为垂足,求
为垂足,求![]() 的最大值;
的最大值;
(3)在(1)的条件下,设点![]() 是抛物线
是抛物线![]() 与
与![]() 的“郡园点”,点
的“郡园点”,点![]() 是抛物线
是抛物线![]() 上一动点,问在抛物线
上一动点,问在抛物线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形?若存在,请直接写出点
为直角顶点的等腰直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系中,正方形![]() 的顶点
的顶点![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点(不与端点
边上一动点(不与端点![]() 重合),连接
重合),连接![]() ,作线段
,作线段![]() 的垂直平分线
的垂直平分线![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
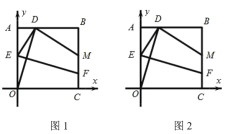
(1)如图1,当点![]() 为线段AB的中点时,求线段
为线段AB的中点时,求线段![]() 的长;
的长;
(2)如图2,若正方形![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,记
,记![]() ,试证明
,试证明![]() 为定值;
为定值;
(3)在(2)的条件下,构造过点C的抛物线![]() 同时满足以下两个条件:
同时满足以下两个条件:
①![]() ;②当
;②当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,求二次项系数
,求二次项系数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题中为真命题的是( )
A.长度为![]() 的三条线段若满足
的三条线段若满足![]() ,则这三条线段一定能组成三角形
,则这三条线段一定能组成三角形
B.一个三角形的三个内角度数之比为3:4:5,则这个三角形是直角三角形
C.正六边形的外角和大于正五边形的外角和
D.若![]() 与
与![]() 相似,且周长相等,则
相似,且周长相等,则![]() 与
与![]() 全等
全等
查看答案和解析>>
科目: 来源: 题型:
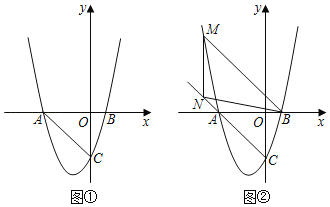
【题目】如图①,抛物线y=x2﹣(a+1)x+a与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.已知△ABC的面积为6.
(1)求这条抛物线相应的函数表达式;
(2)在抛物线上是否存在一点P,使得∠POB=∠CBO,若存在,请求出点P的坐标;若不存在,请说明理由;
(3)如图②,M是抛物线上一点,N是射线CA上的一点,且M、N两点均在第二象限内,A、N是位于直线BM同侧的不同两点.若点M到x轴的距离为d,△MNB的面积为2d,且∠MAN=∠ANB,求点N的坐标.
查看答案和解析>>
科目: 来源: 题型:
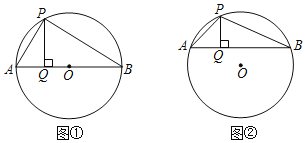
【题目】(1)如图①,AB为⊙O的直径,点P在⊙O上,过点P作PQ⊥AB,垂足为点Q.说明△APQ∽△ABP;
(2)如图②,⊙O的半径为7,点P在⊙O上,点Q在⊙O内,且PQ=4,过点Q作PQ的垂线交⊙O于点A、B.设PA=x,PB=y,求y与x的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙O的半径为1,点A在x轴的正半轴上,B为⊙O上一点,过点A、B的直线与y轴交于点C,且OA2=ABAC.

(1)求证:直线AB是⊙O的切线;
(2)若AB=![]() ,求直线AB对应的函数表达式.
,求直线AB对应的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某农户计划用长12m的篱笆围成一个“日”字形的生物园饲养两种不同的家禽,生物园的一面靠墙,且墙的可利用长度最长为7m.
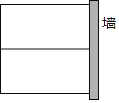
(1)若生物园的面积为9m2,则这个生物园垂直于墙的一边长为多少?
(2)若要使生物园的面积最大,该怎样围?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,转盘A中的6个扇形的面积相等,转盘B中的3个扇形的面积相等.分别任意转动转盘A、B各1次,当转盘停止转动时,将指针所落扇形中的2个数字分别作为平面直角坐标系中一个点的横坐标、纵坐标.
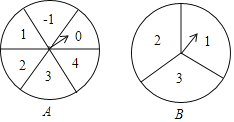
(1)用表格列出这样的点所有可能的坐标;
(2)求这些点落在二次函数y=x2﹣5x+6的图象上的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣16的图象经过点(﹣2,﹣40)和点(6,8).
(1)求这个二次函数图象与x轴的交点坐标;
(2)当y>0时,直接写出自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AC:BC:AB=3:4:5,⊙O沿着△ABC的内部边缘滚动一圈,若⊙O的半径为1,且圆心O运动的路径长为18,则△ABC的周长为_____.
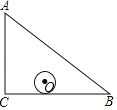
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com