
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 点
点![]() 在
在![]() 上,
上,![]() 点
点![]() 同时从点
同时从点![]() 出发,分别沿
出发,分别沿![]() 以每秒
以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,点
匀速运动,点![]() 到达点
到达点![]() 后立刻以原速度沿
后立刻以原速度沿![]() 向点
向点![]() 运动,点
运动,点![]() 运动到点
运动到点![]() 时停止,点
时停止,点![]() 也随之停止.在点
也随之停止.在点![]() 运动过程中,以
运动过程中,以![]() 为边作正方形
为边作正方形![]() 使它与
使它与![]() 在线段
在线段![]() 的同铡.设
的同铡.设![]() 运动的时间为
运动的时间为![]() 秒,正方形
秒,正方形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() .
.
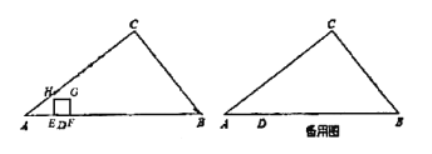
![]() 当
当![]() 时,求正方形
时,求正方形![]() 的顶点刚好落在线段
的顶点刚好落在线段![]() 上时
上时![]() 的值;
的值;
![]() 当
当![]() 时,直接写出当
时,直接写出当![]() 为等腰三角形时
为等腰三角形时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
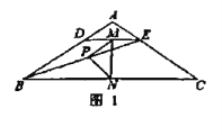
【题目】感知:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 点
点![]() 分别在边
分别在边![]() 上,
上,![]() 连接
连接![]() 点
点![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 与
与![]() 的数量关系是: .
的数量关系是: .
探究:把![]() 绕点
绕点![]() 顺时针方向旋转,如图
顺时针方向旋转,如图![]() ,连接
,连接![]()
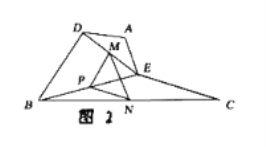
![]() 证明:
证明: ![]()
![]() 的度数为 _
的度数为 _![]()
应用:把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() 面积的最大值为___________.
面积的最大值为___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
![]() 抛物线的开口向____ 、对称轴为直线_ _、顶点坐标__ _;
抛物线的开口向____ 、对称轴为直线_ _、顶点坐标__ _;
![]() 当
当![]() ___ _时,函数有最___ 值,是__ _;
___ _时,函数有最___ 值,是__ _;
![]() 当
当![]() _ _ ______时,
_ _ ______时,![]() 随
随![]() 的增大而增大;当
的增大而增大;当![]() ____ __时,
____ __时,![]() 随
随![]() 的增大而减小;
的增大而减小;
![]() 该函数图象可由
该函数图象可由![]() 的图象经过怎样的平移得到的?
的图象经过怎样的平移得到的?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读与应用:同学们,你们已经知道![]() ,即
,即![]() .所以
.所以![]() (当且仅当
(当且仅当![]() 时取等号).
时取等号).
阅读1:若![]() 为实数,且
为实数,且![]() (当且仅当
(当且仅当![]() 时取等号).
时取等号).
阅读2:若函数![]() (
(![]() ,
,![]() ,
,![]() 为常数).由阅读1结论可知:
为常数).由阅读1结论可知:![]() 即
即![]() ,∴当
,∴当![]() 即
即![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() .
.
阅读理解上述内容,解答下列问题:
问题1:若函数![]() ,则
,则![]() = 时,函数
= 时,函数![]() 的最小值为 .
的最小值为 .
问题2:已知一个矩形的面积为4,其中一边长为![]() ,则另一边长为
,则另一边长为![]() ,周长为
,周长为![]() ,求当
,求当![]() 时,矩形周长的最小值为 .
时,矩形周长的最小值为 .
问题3:求代数式![]() 的最小值.
的最小值.
问题4:建造一个容积为8立方米,深2米的长方体无盖水池,池底和池壁的造价分别为每平方米![]() 米,水池总造价为
米,水池总造价为![]() (元),求当
(元),求当![]() 为多少时,水池总造价
为多少时,水池总造价![]() 最低?最低是多少?
最低?最低是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数且
为常数且![]() )中,当
)中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .请对该函数及其图像进行如下探究:
.请对该函数及其图像进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量![]() 的取值范围:
的取值范围:
(2)请在下列直角坐标系中画出该函数的图像:
列表如下:
x | … | -4 | -3 | -2 | -1 | 0 |
|
| 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | … |
描点连线:
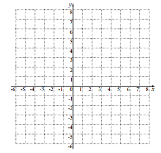
(3)请结合所画函数图象,写出函数图象的两条性质
(4)请你在上方直角坐标系中画出函数![]() 的图像,结合上述函数的图像,写出不等式
的图像,结合上述函数的图像,写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目: 来源: 题型:
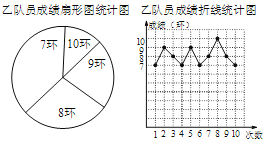
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员举行了一次选拔赛,要求这两名队员各射击10次.比赛结束后,根据比赛成绩情况,将甲、乙两名队员的比赛成绩制成了如下的统计图(表):
甲队员的成绩统计表
成绩(单位:环) | 7 | 8 | 9 | 10 |
次数(单位:次) | 5 | 1 | 2 | 2 |
(1)在图1中,求“8环”所在扇形的圆心角的度数;
(2)经过整理,得到的分析数据如表,求表中的a、b、c的值.
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 | c |
乙 | a | b | 7 | 1 |
(3)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.
查看答案和解析>>
科目: 来源: 题型:
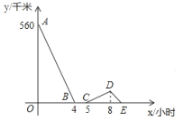
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为![]() 小时,两车之间的距离为
小时,两车之间的距离为![]() 千米,图中折线表示
千米,图中折线表示![]() 与
与![]() 之间的函数图象.当快车到达甲地时,慢车离甲地的距离为__________千米.
之间的函数图象.当快车到达甲地时,慢车离甲地的距离为__________千米.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com