
科目: 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )

A. π B. ![]() C. 3+π D. 8﹣π
C. 3+π D. 8﹣π
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=BC,A、B的坐标分别为(0,4),(-2,4),将△ABC绕点P旋转180°后得到△A′B′C′,其中点B的对应点B′的坐标为(2,2).
(1)求出点C的坐标;
(2)求点P的坐标,并求出点C的对应点C′的坐标.

查看答案和解析>>
科目: 来源: 题型:
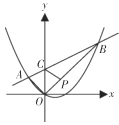
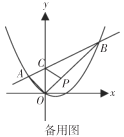
【题目】如图,在平面直角坐标系中,抛物线![]() 上有两点
上有两点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 到两坐标轴的距离相等.点
到两坐标轴的距离相等.点![]() 到两坐标轴的距离也相等.
到两坐标轴的距离也相等.
(1)求点![]() ,
,![]() 的坐标并直接写出
的坐标并直接写出![]() 的形状;
的形状;
(2)若点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,当
,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上一动点,当
轴上一动点,当![]() 是以
是以![]() 为斜边的直角三角形时,求点
为斜边的直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
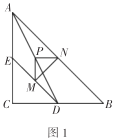
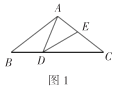
问题情境:在综合与实践课上,老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合,并让一个三角板固定,另一个绕直角顶点旋转”为主题开展数学活动,如图1,三角板![]() 和三角板
和三角板![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,连接
上,连接![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.试判断线段
的中点.试判断线段![]() 与
与![]() 的数量关系和位置关系.
的数量关系和位置关系.
探究展示:勤奋小组发现,![]() ,
,![]() .并展示了如下的证明方法:
.并展示了如下的证明方法:
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .
.
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .(依据1)
.(依据1)
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .(依据2)
.(依据2)
∴![]() .∴
.∴![]() .
.
反思交流:
(1)①上述证明过程中的“依据1”,“依据2”分别是指什么?
②试判断图1中,![]() 与
与![]() 的位置关系,请直接回答,不必证明;
的位置关系,请直接回答,不必证明;
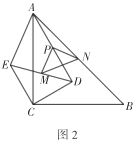
(2)创新小组受到勤奋小组的启发,继续进行探究,把![]() 绕点
绕点![]() 逆时针方向旋转到如图2的位置,发现
逆时针方向旋转到如图2的位置,发现![]() 是等腰直角三角形,请你给出证明;
是等腰直角三角形,请你给出证明;
(3)缜密小组的同学继续探究,把![]() 绕点
绕点![]() 在平面内自由旋转,当
在平面内自由旋转,当![]() ,
,![]() 时,求
时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产的商品的市场指导价为每件150元,公司的实际销售价格可以浮动![]() 个百分点[即销售价格
个百分点[即销售价格![]() ],经过市场调研发现,这种商品的日销售量
],经过市场调研发现,这种商品的日销售量![]() (件)与销售价格浮动的百分点
(件)与销售价格浮动的百分点![]() 之间的函数关系如下:
之间的函数关系如下:
浮动 | 0 | 1 | 2 | 3 | … |
销售量 | 24 | 22 | 20 | 18 | … |
若该公司按浮动![]() 个百分点的价格出售,每件商品仍可获利10%.
个百分点的价格出售,每件商品仍可获利10%.
(1)求该公司生产每件商品的成本为多少元?
(2)当实际销售价格定为多少元时,日销售利润为660元?[说明:日销售利润![]() (销售价格
(销售价格![]() 成本)
成本)![]() 日销售量];
日销售量];
(3)该公司决定每销售一件商品就捐赠![]() 元利润(
元利润(![]() )给希望工程,公司通过销售记录发现,当价格浮动的百分点大于
)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于![]() 时,扣除捐赠后的日销售利润随
时,扣除捐赠后的日销售利润随![]() 的增大而减小,直接写出
的增大而减小,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边作
为边作![]() ,交
,交![]() 边于点
边于点![]() .设
.设![]() ,
,![]() .今天我们将根据学习函数的经验,研究函数值
.今天我们将根据学习函数的经验,研究函数值![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)通过计算,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | 4.5 | 5 | 5.5 |
| 3.3125 | 2.75 | 2.3125 | 2 | 2.3125 | 2.75 | 3.3125 |
请你补全表格;
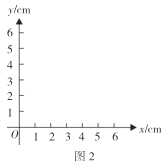
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象;
(4)根据图象,请写出该函数的一条性质.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了丰富居民的文化生活.某社区开展跳舞、绘画、游泳、唱歌等活动来让居民娱乐.为了解居民对跳舞、绘画、游泳、唱歌这四种活动(以下分别用![]() ,
,![]() ,
,![]() ,
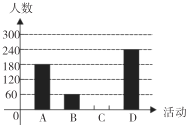
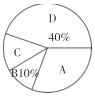
,![]() 表示这四种不同活动)的喜爱情况,在“五一”劳动节期间对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
表示这四种不同活动)的喜爱情况,在“五一”劳动节期间对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整;
(3)若居民区有8000人,请估计爱唱歌的人数?
(4)在“五—”劳动节期间,该社区针对跳舞、绘画、游泳、唱歌起带头作用的居民各选举一名进行奖励,同时随机抽取两人进行现场展示,请用列表或画树状图法求恰好选中跳舞和绘画的概率.(跳舞、绘画、游泳、唱歌分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com