
科目: 来源: 题型:
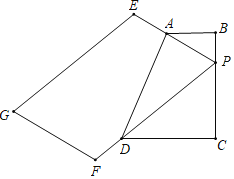
【题目】在四边形ABCD中,AB∥CD,BC⊥CD,AB=2,CD=3,在BC上取点P(P与B、C不重合)连接PA延长至E,使PA=2AE,连接PD并延长至F,使PD=3FD,以PE、PF为边作平行四边形,另一个顶点为G,则PG长度的最小值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy 中,点A 的坐标为(1,0),P 是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).若点P到x轴的距离为![]() ,则m+n 的最小值为___.
,则m+n 的最小值为___.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() .
.
(1)抛物线的对称轴为直线________.
(2)当![]() 时,函数值
时,函数值![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 和
和![]() 的值.
的值.
(3)当![]() 时,解决下列问题.
时,解决下列问题.
①抛物线上一点![]() 到
到![]() 轴的距离为6,求点
轴的距离为6,求点![]() 的坐标.
的坐标.
②将该抛物线在![]() 间的部分记为
间的部分记为![]() ,将
,将![]() 在直线
在直线![]() 下方的部分沿
下方的部分沿![]() 翻折,其余部分保持不变,得到的新图象记为
翻折,其余部分保持不变,得到的新图象记为![]() ,设
,设![]() 的最高点、最低点的纵坐标分别为
的最高点、最低点的纵坐标分别为![]() 、
、![]() ,若
,若![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,点
,点![]() 是射线
是射线![]() 上的一点,且
上的一点,且![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).

(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值.
的值.
(3)当矩形![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)点![]() 与点
与点![]() 同时出发,在线段
同时出发,在线段![]() 上以每秒2个单位长度的速度沿
上以每秒2个单位长度的速度沿![]() 往返运动,连结
往返运动,连结![]() 、
、![]() ,当点
,当点![]() 停止时点
停止时点![]() 也随之停止,直接写出矩形
也随之停止,直接写出矩形![]() 面积是
面积是![]() 面积的4倍时
面积的4倍时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(感知)如图1,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,易知
,易知![]() ,得到点
,得到点![]() 的坐标为
的坐标为![]() .
.
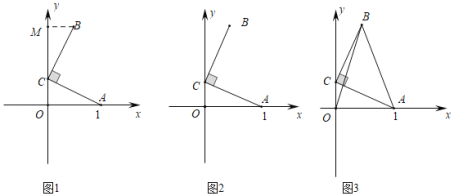
(探究)如图2,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() .
.
(1)求点![]() 的坐标.(用含
的坐标.(用含![]() 的代数式表示)
的代数式表示)
(2)求出BC所在直线的函数表达式.
(拓展)如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,将线段
轴上,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() ,连结
,连结![]() 、
、![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两个工程队共同承建一段公路路基工程,由乙队先单独施工40天后,甲乙两队共同施工.甲队每天挖土0.425万立方米,乙队工作效率保持不变,设甲、乙两队在此公路施工中的挖土总量![]() (万立方米)与工作时间
(万立方米)与工作时间![]() (天)的函数图象如图所示.
(天)的函数图象如图所示.
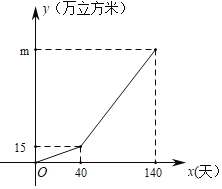
(1)求乙队每天的挖土量;
(2)求此次任务的挖土总量![]() ;
;
(3)求甲、乙两队共同施工时![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解九年级学生的物理实验操作情况,进行了抽样调查.随机抽取了40名同学进行实验操作,成绩如下:
21 | 22 | 22 | 23 | 23 | 23 | 23 | 22 | 24 | 24 |
25 | 23 | 21 | 25 | 24 | 25 | 23 | 22 | 24 | 25 |
23 | 23 | 24 | 24 | 24 | 24 | 23 | 25 | 25 | 21 |
21 | 23 | 23 | 24 | 25 | 24 | 22 | 24 | 22 | 24 |
整理上面数据,得到如下统计图:

样本数据的平均数、众数、中位数如表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | m | 24 | 23 |
根据以上信息,解答下列问题:
(1)如表中平均数![]() 的值为_______;
的值为_______;
(2)扇形统计图中“ 24分”部分的圆心角大小为_______度;
(3)根据样本数据,请估计该校九年级320名学生中物理实验操作得满分的学生人数.
查看答案和解析>>
科目: 来源: 题型:
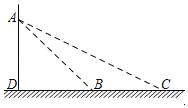
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
查看答案和解析>>
科目: 来源: 题型:
【题目】【探索发现】
如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
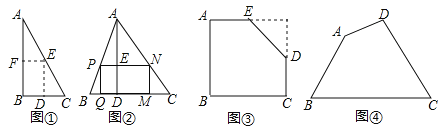
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com