
科目: 来源: 题型:
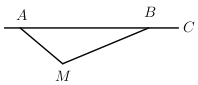
【题目】根据道路管理规定,在广州某段笔直公路上行驶的车辆,限速40千米/时;已知交警测速点![]() 到该公路
到该公路![]() 点的距离为
点的距离为![]() 米,
米,![]() ,
,![]() (如图所示),现有一辆汽车由
(如图所示),现有一辆汽车由![]() 往
往![]() 方向匀速行驶,测得此车从
方向匀速行驶,测得此车从![]() 点行驶到
点行驶到![]() 点所用的时间为2秒.
点所用的时间为2秒.
(1)求测速点![]() 到该公路的距离.
到该公路的距离.
(2)通过计算判断此车是否超速.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】今年4月份,某校九年级学生参加了广州市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
分组 | 分数段(分) | 频数 |
|
| 2 |
|
| 5 |
|
| 15 |
|
|
|
|
| 10 |
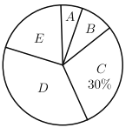
(1)求全班学生人数和![]() 的值.
的值.
(2)直接写出该班学生的中考体育成绩的中位数落在哪个分数段.
(3
查看答案和解析>>
科目: 来源: 题型:
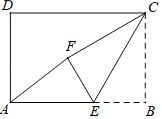
【题目】如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是_____(写出所有正确结论的序号)
①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF=![]() ;
;
③当A、F、C三点共线时,AE=![]() ;
;
④当A、F、C三点共线时,△CEF≌△AEF.
查看答案和解析>>
科目: 来源: 题型:
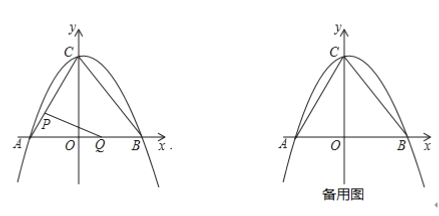
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与坐标轴交于
的图像与坐标轴交于![]() 三点,其中点
三点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .动点
.动点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 作匀速运动;同时,动点
作匀速运动;同时,动点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为
作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为![]() 秒.连接
秒.连接![]() .
.
(1)填空:![]() _________,
_________,![]() ________;
________;
(2)在点![]() 运动过程中,
运动过程中,![]() 可能是直角三角形吗?请说明理由;
可能是直角三角形吗?请说明理由;
(3)在![]() 轴下方,该二次函数的图象上是否存在点
轴下方,该二次函数的图象上是否存在点![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形?若存在,请求出运动时间
为直角顶点的等腰直角三角形?若存在,请求出运动时间![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂有甲种原料69千克,乙种原料52千克,现计划用这两种原料生产A,B两种型号的产品共80件,已知每件A型号产品需要甲种原料0.6千克,乙种原料0.9千克;每件B型号产品需要甲种原料1.1千克,乙种原料0.4千克.请解答下列问题:
(1)该工厂有哪几种生产方案?
(2)在这批产品全部售出的条件下,若1件A型号产品获利35元,1件B型号产品获利25元,(1)中哪种方案获利最大?最大利润是多少?
(3)在(2)的条件下,工厂决定将所有利润的25%全部用于再次购进甲、乙两种原料,要求每种原料至少购进4千克,且购进每种原料的数量均为整数.若甲种原料每千克40元,乙种原料每千克60元,请直接写出购买甲、乙两种原料之和最多的方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】小红参加学校组织的庆祝党的十九大胜利召开知识竞赛,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,可是小红这两道题都不会,不过竞赛规则规定每位选手有两次求助机会,使用“求助”一次可以让主持人去掉其中一题的一个错误选项,主持人提醒小红可以使用两次“求助”.
(1)如果小红两次“求助”都在第一道题中使用,那么小红通关的概率是 .
(2)如果小红将每道题各用一次“求助”,请用树状图或者列表来分析她顺序通关的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,某校学生会为了调查学生对雾霾天气知识的了解程度,随机抽取了该校的n名学生做了一次跟踪调查,将调查结果分为四个等级:(A)非常了解.(B)比较了解.(C)基本了解.(D)不了解,并将调查结果绘制成如下两幅不完整统计图.
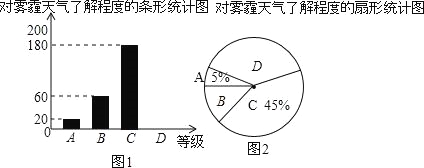
根据统计图提供的信息,解答下列问题:
(1)求n的值;
(2)在调查的n名学生中,对雾霾天气知识不了解的学生有 人,并将条形统计图补充完整.
(3)估计该校1500名学生中,对雾霾天气知识比较了解的学生人数.
查看答案和解析>>
科目: 来源: 题型:
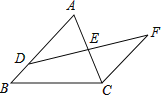
【题目】如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.
(1)求证:AD=CF.
(2)连接AF,CD,求证:四边形ADCF为平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com