
科目: 来源: 题型:
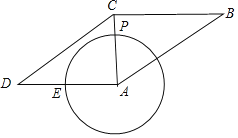
【题目】如图,已知P是半径为3的⊙A上一点,延长AP到点C,使AC=4,以AC为对角线作ABCD,AB=4![]() ,⊙A交边AD于点E,当ABCD面积为最大值时,
,⊙A交边AD于点E,当ABCD面积为最大值时,![]() 的长为( )
的长为( )
A.![]() πB.πC.
πB.πC.![]() πD.3π
πD.3π
查看答案和解析>>
科目: 来源: 题型:
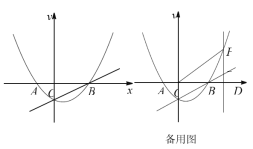
【题目】如图,抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为抛物线上的一个动点,过点
为抛物线上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线解析式;
(2)若点![]() 在第一象限内,当
在第一象限内,当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(3)将![]() 绕平面直角坐标系中某点逆时针旋转
绕平面直角坐标系中某点逆时针旋转![]() ,对应点为
,对应点为![]() ,
,![]() ,
,![]() ,当
,当![]() 中有两个顶点落在抛物线上时,直接写出
中有两个顶点落在抛物线上时,直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
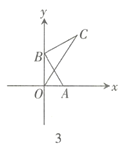
【题目】(1)问题发现
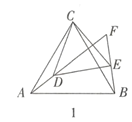
如图1,![]() 和
和![]() 均为等边三角形,直线
均为等边三角形,直线![]() 和直线
和直线![]() 交于点
交于点![]() .
.
填空:①![]() 的度数是 ;
的度数是 ;
②线段![]() ,
,![]() 之间的数量关系为 .
之间的数量关系为 .
(2)类比探究
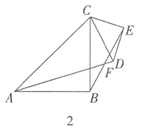
如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 和直线
和直线![]() 交于点
交于点![]() .请判断
.请判断![]() 的度数及线段
的度数及线段![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)解决问题
如图3,在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 为
为![]() 轴上任意一点,连接
轴上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市中招体育测试改革,其中篮球和足球作为选考项目,某商店抓住这一商机决定购进一批篮球和足球共200个,这两种球的进价和售价如下表所示:
篮球 | 足球 | |
进价(元/个) | 180 | 150 |
售价(元/个) | 250 | 200 |
(1)若商店计划销售完这批球后能获利11600元,问篮球和足球应分别购进多少个?
(2)设购进篮球![]() 个,获利为
个,获利为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(3)若商店计划投入资金不多于31560元且销售完这批球后商店获利不少于11000元,请问有哪几种购球方案,并写出获利最大的购球方案.
查看答案和解析>>
科目: 来源: 题型:
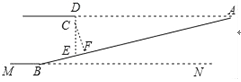
【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈3.16)
≈3.16)
查看答案和解析>>
科目: 来源: 题型:
【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了两幅统计图:
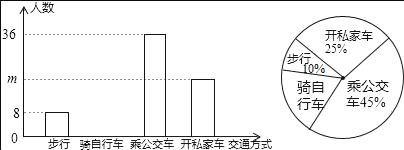
(1)样本中的总人数为 人;扇形统计十图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有1000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
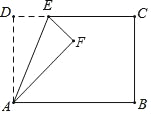
查看答案和解析>>
科目: 来源: 题型:
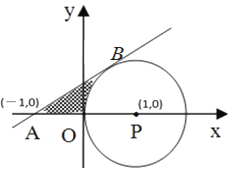
【题目】如图,在平面直角坐标系中,以(1,0)为圆心的⊙P与y轴相切于原点O,过点A(-1,0)的直线AB与⊙P相切于点B.
(1)求AB的长.
(2)求AB、OA与![]() 所围成的阴影部分面积.
所围成的阴影部分面积.
(3)求直线AB的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
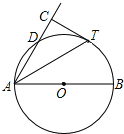
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,CT=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com