
科目: 来源: 题型:
【题目】某商场经营一种商品,进价是每千克30元,根据市场调查发现,每日的销售量![]() (千克)与售价
(千克)与售价![]() (元/千克)满足一次函数关系.下表记录的是某两日的有关数据:
(元/千克)满足一次函数关系.下表记录的是某两日的有关数据:
| 35 | 40 |
| 850 | 800 |
(1)求![]() 与
与![]() 的函数关系式(不求自变量的取值范围);
的函数关系式(不求自变量的取值范围);
(2)在销售过程中销售单价不低于成本价,且不高于80元,某日该商场出售这种商品获得了14000元的利润,求该商品的售价?
(3)若某日该商场这种商品的销售量不少于500千克,求这一天该商场销售这种商品获得的最大利润为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校现有九年级学生800名,为了了解这些学生的体质健康情况,学校在开学初从中随机抽取部分学生进行体能测试(测试结果分成优秀、良好、合格、不合格四个等级),并将测试结果绘制成如图所示两幅不完整的统计图,请结合图中提供的信息解答下列问题:
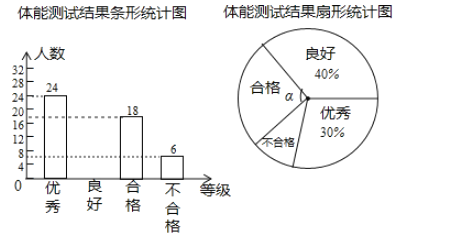
(1)本次抽取的学生人数共有____名,在扇形统计图中,“合格”等级所对应的圆心角![]() 的度数是______;
的度数是______;
(2)补全条形统计图;
(3)估计九年级学生中达到“合格”以上(含合格)等级的学生一共有多少名?
(4)若抽取的学生中,恰好有九年级(1)班的2名男生,2名女生,现要从这4人中随机抽取2人担任组长工作,请用列表法或树状图法求所抽取的2名学生中至少有1名女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目: 来源: 题型:
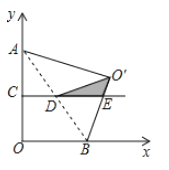
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 为
为![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折得
翻折得![]() ,点
,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,点
为直角三角形时,点![]() 坐标为_______.
坐标为_______.
查看答案和解析>>
科目: 来源: 题型:
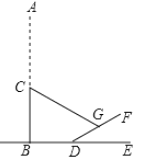
【题目】如图,一棵与地面垂直的笔直大树![]() ,在
,在![]() 点处被大风折断后,
点处被大风折断后,![]() 部分倒下,树的顶端
部分倒下,树的顶端![]() 与斜坡
与斜坡![]() 上的点
上的点![]() 重合(
重合(![]() 都保持笔直),经测量
都保持笔直),经测量![]() ,
,![]() ,则树高
,则树高![]() 为_______米(保留根号).
为_______米(保留根号).
查看答案和解析>>
科目: 来源: 题型:
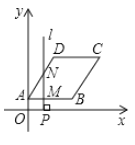
【题目】如图,在平面直角坐标私法中,四边形![]() 是菱形,
是菱形,![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() ,
,![]() ,垂直于
,垂直于![]() 轴的直线
轴的直线![]() 从
从![]() 轴出发,沿
轴出发,沿![]() 轴正方向以每秒1个单位长度的速度向右平移,设直线
轴正方向以每秒1个单位长度的速度向右平移,设直线![]() 与菱形
与菱形![]() 的两边分别交于点
的两边分别交于点![]() (点
(点![]() 在点
在点![]() 的上方),连接
的上方),连接![]() ,若
,若![]() 的面积为
的面积为![]() ,直线
,直线![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ),则
),则![]() 与
与![]() 的函数图象大致是( )
的函数图象大致是( )
A.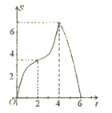 B.
B.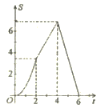 C.
C.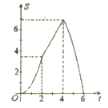 D.
D.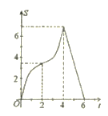
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,对于点![]() 和点
和点![]() ,给出如下定义:
,给出如下定义:
若![]() ,则称点
,则称点![]() 为点
为点![]() 的限变点.
的限变点.
例如:点![]() 的限变点的坐标为
的限变点的坐标为![]() ,点
,点![]() 的限变点的坐标是
的限变点的坐标是![]() .
.
(1)①![]() 的限变点的坐标是____________.
的限变点的坐标是____________.
②若点![]() 在函数
在函数![]() 图象上,其限变点
图象上,其限变点![]() 在函数
在函数![]() 的图象上,则函数
的图象上,则函数![]() 的函数值
的函数值![]() 随
随![]() 的增大而增大时自变量
的增大而增大时自变量![]() 的取值范围是____________.
的取值范围是____________.
(2)若点![]() 在函数
在函数![]() 的图象上,其限变点
的图象上,其限变点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
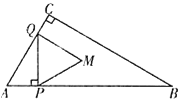
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发以每秒2个单位的速度沿
出发以每秒2个单位的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() ,当点
,当点![]() 不和
不和![]() 的顶点重合时,以
的顶点重合时,以![]() 为边作等边三角形
为边作等边三角形![]() ,使点
,使点![]() 和点
和点![]() 在直线
在直线![]() 的同侧,设点
的同侧,设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
(1)求等边三角形![]() 的边长(用含
的边长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边
的边![]() 上时,求
上时,求![]() 的值;
的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)作直线![]() ,设点
,设点![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() ,直接写出
,直接写出![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,△MNQ中,MQ≠NQ.
(1)请你以MN为一边,在MN的同侧构造一个与△MNQ全等的三角形,画出图形,并简要说明构造的方法;
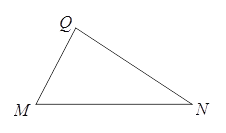
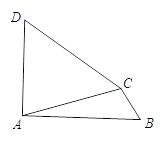
(2)参考(1)中构造全等三角形的方法解决下面问题:
如图,在四边形ABCD中,![]() ,∠B=∠D.求证:CD=AB.
,∠B=∠D.求证:CD=AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com