
科目: 来源: 题型:
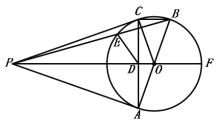
【题目】如图,⊙![]() 是△
是△![]() 的外接圆,
的外接圆,![]() 为直径,点
为直径,点![]() 是⊙
是⊙![]() 外一点,且
外一点,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() .
.
⑴.证明:![]() =
=![]() ;
;
⑵.若![]() ,证明:
,证明:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑶.在⑵的条件下,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,连接
,连接![]() ;若
;若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”;数形结合是解决数学问题的重要思想方法.例如,代数式![]() 的几何意义是数轴上
的几何意义是数轴上![]() 所对应的点与2所对应的点之间的距离;因为
所对应的点与2所对应的点之间的距离;因为![]() ,所以
,所以![]() 的几何意义就是数轴上
的几何意义就是数轴上![]() 所对应的点与
所对应的点与![]() 所对应的点之间的距离.
所对应的点之间的距离.
⑴. 发现问题:代数式![]() 的最小值是多少?
的最小值是多少?
⑵. 探究问题:如图,点![]() 分别表示的是
分别表示的是![]() ,
,![]() .
.
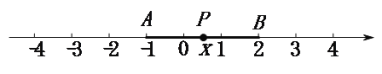
∵![]() 的几何意义是线段
的几何意义是线段![]() 与
与![]() 的长度之和
的长度之和
∴当点![]() 在线段
在线段![]() 上时,
上时,![]() ;当点点
;当点点![]() 在点
在点![]() 的左侧或点
的左侧或点![]() 的右侧时
的右侧时 ![]()
∴![]() 的最小值是3.
的最小值是3.
⑶.解决问题:
①.![]() 的最小值是 ;
的最小值是 ;
②.利用上述思想方法解不等式:![]()
![]()
③.当![]() 为何值时,代数式
为何值时,代数式![]() 的最小值是2.
的最小值是2.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品,新冠疫情期间,为了减少库存,甲、乙两家商场打折促销,甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.
⑴.以![]() (单位:元)表示商品原价,
(单位:元)表示商品原价,![]() (单位:元)表示实际购物金额,分别就两家商场的让利方式写出
(单位:元)表示实际购物金额,分别就两家商场的让利方式写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
⑵.新冠疫情期间如何选择这两家商场去购物更省钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了响应市政府号召,在“创文创卫”活动周中,设置了“![]() :文明礼仪;
:文明礼仪;![]() :环境保护;
:环境保护;![]() ;卫生保洁;
;卫生保洁;![]() :垃圾分类 ”四个主题,每个学生选一个主题参与;为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
:垃圾分类 ”四个主题,每个学生选一个主题参与;为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
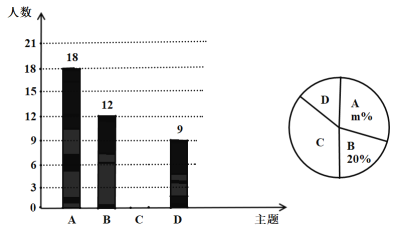
⑴.本次调查的学生人数是 人,![]() = ;
= ;
⑵.请补全条形统计图;
⑶.学校要求每位同学从星期一至星期五选择两天参加活动,如果小张同学随机选择连续两天,其中有一天是星期一的概率是 ;小李同学星期五要参加市演讲比赛,他在其余四天中随机选择两天,其中一天是星期三的概率是 .
查看答案和解析>>
科目: 来源: 题型:
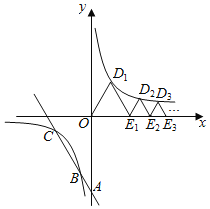
【题目】如图, 直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() 在第三象限交于
在第三象限交于![]() 两点,且
两点,且 ![]() ;下列等边三角形
;下列等边三角形![]() ,
,![]() ,
,![]() ,……的边
,……的边![]() ,
,![]() ,
,![]() ,……在
,……在![]() 轴上,顶点
轴上,顶点![]() ……在该双曲线第一象限的分支上,则
……在该双曲线第一象限的分支上,则![]() = ____,前25个等边三角形的周长之和为 _______.
= ____,前25个等边三角形的周长之和为 _______.
查看答案和解析>>
科目: 来源: 题型:
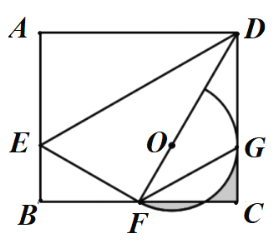
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 上的一点,连接
上的一点,连接![]() ,将△
,将△![]() 进行翻折,恰好使点
进行翻折,恰好使点![]() 落在
落在![]() 的中点
的中点![]() 处,在
处,在![]() 上取一点
上取一点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作半圆与
的长为半径作半圆与![]() 相切于点
相切于点![]() ;若
;若![]() ,则图中阴影部分的面积为 ____ .
,则图中阴影部分的面积为 ____ .
查看答案和解析>>
科目: 来源: 题型:
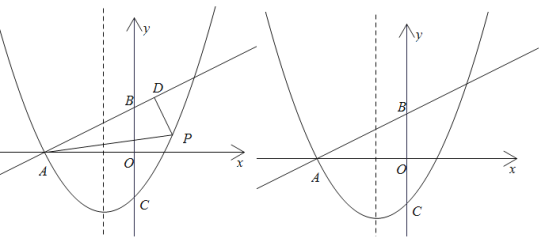
【题目】如图,直线![]() 交
交![]() 轴于点A,交
轴于点A,交![]() 轴于点B,抛物线
轴于点B,抛物线![]() 经过点A,交
经过点A,交![]() 轴于点
轴于点![]() ,点P为直线AB下方抛物线上一动点,过点P作
,点P为直线AB下方抛物线上一动点,过点P作![]() 于D,连接AP.
于D,连接AP.
(1)求抛物线的解析式;
(2)若以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点P的坐标;
相似,求点P的坐标;
(3)将![]() 绕点A旋转,当点O的对应点
绕点A旋转,当点O的对应点![]() 落在抛物线的对称轴上时,请直接写出点B的对应点
落在抛物线的对称轴上时,请直接写出点B的对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
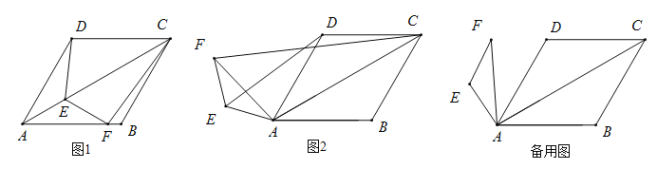
【题目】如图1,在菱形ABCD中,![]() ,点E,F分别是AC,AB上的点,且
,点E,F分别是AC,AB上的点,且![]() ,猜想:
,猜想:
①![]() 的值是_______;
的值是_______;
②直线DE与直线CF所成的角中较小的角的度数是_______.
(2)类比探究:如图2,将绕![]() 点A逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.
点A逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.
(3)拓展延伸:
在![]() 绕点A旋转的过程中,当
绕点A旋转的过程中,当![]() 三点共线时,请直接写出CF的长.
三点共线时,请直接写出CF的长.
查看答案和解析>>
科目: 来源: 题型:
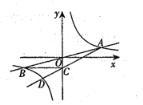
【题目】如图,在平面直角坐标系中,双曲线![]() 与直线
与直线![]() 相交于点
相交于点![]() 和B,过B点作
和B,过B点作![]() 轴于点C,连接AC,已知
轴于点C,连接AC,已知![]() .
.
(1)求![]() 的值;
的值;
(2)延长AC交双曲线于另一点D,求D的的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com