
科目: 来源: 题型:
【题目】已知二次函数图象过点A(-2,0),B(4,0),C(0,4)
(1)求二次函数的解析式;
(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标,若不存在,请说明理由.
(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角![]() ,且tan
,且tan![]() =
=![]() ,求点K的坐标.
,求点K的坐标.

查看答案和解析>>
科目: 来源: 题型:
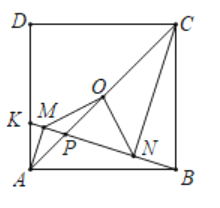
【题目】如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.
(1)求证:AM=BN;
(2)请判断△OMN的形状,并说明理由;
(3)若点K在线段AD上运动(不包括端点),设AK=x,△OMN的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且△OMN的面积为![]() ,请直接写出AK长.
,请直接写出AK长.
查看答案和解析>>
科目: 来源: 题型:
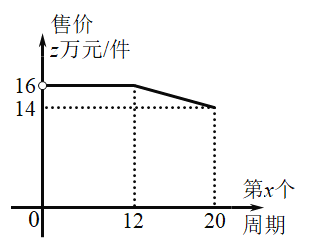
【题目】某工厂计划在每个生产周期内生产并销售完某型设备,设备的生产成本为10万元/件(1)如图,设第x(0<x≤20)个生产周期设备售价z万元/件,z与x之间的关系用图中的函数图象表示,求z关于x的函数解析式(写出x的范围).
(2)设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0<x≤20).在(1)的条件下,工厂在第几个生产周期创造的利润最大?最大为多少万元?(利润=收入-成本)
查看答案和解析>>
科目: 来源: 题型:
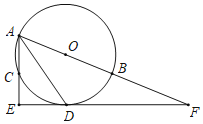
【题目】如图,点A,B,C是半径为2的⊙O上三个点,AB为直径,∠BAC的平分线交圆于点D,过点D作AC的垂线交AC得延长线于点E,延长线ED交AB得延长线于点F.
(1)判断直线EF与⊙O的位置关系,并证明.
(2)若DF=![]() ,求tan∠EAD的值.
,求tan∠EAD的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年,全球疫情大爆发,我国派遣医疗专家组对一些国家进行医疗援助,某批次派出20人组成的专家组,分别赴A、B、C、D四个国家开展援助工作,七人员分布情况如统计图(不完整)所示:
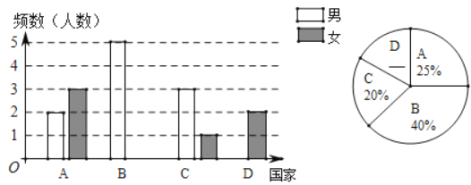
(1)计算赴B国女专家和D国男专家的人数,并将条形统计图补充完整;
(2)根据需要,从赴A国的专家,随机抽取两名专家对当地医疗团队进行培训,求所抽取的两名专家恰好是一男一女的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】关于二次函数![]() 的三个结论:①对任意实数m,都有
的三个结论:①对任意实数m,都有![]() 与
与![]() 对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则
对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则![]() 或
或![]() ;③若抛物线与x轴交于不同两点A,B,且AB≤6,则
;③若抛物线与x轴交于不同两点A,B,且AB≤6,则![]() 或
或![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目: 来源: 题型:
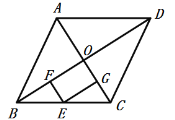
【题目】如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC单位中点,过点E作EF⊥BD于F,EG⊥AC与G,则四边形EFOG的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,将函数![]() 为常数)的图象记为
为常数)的图象记为![]() 图象
图象![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为![]() .
.
(1)若点![]() 在图象
在图象![]() 上,求
上,求![]() 的值;
的值;
(2)求![]() 的最小值;
的最小值;
(3)当直线![]() 的图象与函数
的图象与函数![]() 为常数)的图像只有一个公共点时,求
为常数)的图像只有一个公共点时,求![]() 的取值范围;
的取值范围;
(4)若![]() 点
点![]() 在图象
在图象![]() 上,且点
上,且点![]() 的横坐标为
的横坐标为![]() 点
点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .当点
.当点![]() 不在坐标轴上时,以点
不在坐标轴上时,以点![]() 为顶点构造矩形
为顶点构造矩形![]() 使点
使点![]() 落在
落在![]() 轴上.当图象
轴上.当图象![]() 与矩形
与矩形![]() 的边有两个公共点时,直接写出
的边有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 于点
于点![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() ,以
,以![]() 为边作
为边作![]() 使
使![]() 点
点![]() 在点
在点![]() 的下方,且
的下方,且![]() ,设
,设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
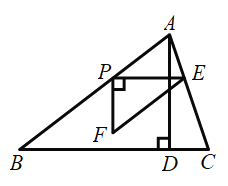
(1)![]() 的长为 ;
的长为 ;
(2)当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值;
的值;
(3)当![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)若射线![]() 与边
与边![]() 交于点
交于点![]() 连结
连结![]() ,当
,当![]() 的垂直平分线经过
的垂直平分线经过![]() 的顶点时,直接写出
的顶点时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】[问题解答]
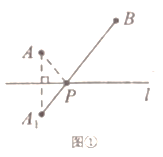
两个城镇![]() 与一条公路
与一条公路![]() 位置如图①所示.现电信部门需在公路
位置如图①所示.现电信部门需在公路![]() 上修建一座信号发射塔
上修建一座信号发射塔![]() 要求发射塔
要求发射塔![]() 到两个城镇
到两个城镇![]() 与
与![]() 的距离之和最短.
的距离之和最短.
解:点![]() 作关于直线
作关于直线![]() 的对称点
的对称点![]() 连结
连结![]() ,
,
与直线![]() 的交点即为所求的点
的交点即为所求的点![]() .
.
![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() 直线
直线![]() 垂直平分
垂直平分![]()
![]()
![]()
![]() 点
点![]() 即为所求的点。(两点之间线段最短)
即为所求的点。(两点之间线段最短)
请根据以上问题解答,完成下列问题.
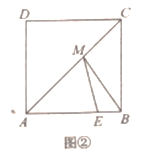
[方法运用]如图②,在正方形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,点
上,点![]() 在对角线AC上,
在对角线AC上,
(1)当点![]() 是边
是边![]() 的中点时,则
的中点时,则![]() 的最小值为 ;
的最小值为 ;
(2)若![]() 求
求![]() 周长的最小值.
周长的最小值.
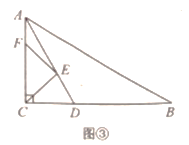
[拓展提升]如图③,在![]() 中,
中,![]() ,AD平分
,AD平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 分别在
分别在![]() 上,则
上,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com