
科目: 来源: 题型:
【题目】某生产商存有1200千克![]() 产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产
产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产![]() 产品,
产品,![]() 产品售价为200元/千克.经市场调研发现,
产品售价为200元/千克.经市场调研发现,![]() 产品存货的处理价格
产品存货的处理价格![]() (元/千克)与处理数量
(元/千克)与处理数量![]() (千克)满足一次函数关系(
(千克)满足一次函数关系(![]() ),且得到表中数据.
),且得到表中数据.
|
|
200 | 350 |
400 | 300 |
(1)请求出处理价格![]() (元千克)与处理数量
(元千克)与处理数量![]() (千克)之间的函数关系;
(千克)之间的函数关系;
(2)若![]() 产品生产成本为100元千克,
产品生产成本为100元千克,![]() 产品处理数量为多少千克时,生产
产品处理数量为多少千克时,生产![]() 产品数量最多,最多是多少?
产品数量最多,最多是多少?
(3)由于改进技术,![]() 产品的生产成本降低到了
产品的生产成本降低到了![]() 元/千克,设全部产品全部售出,所得总利润为
元/千克,设全部产品全部售出,所得总利润为![]() (元),若
(元),若![]() 时,满足
时,满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目: 来源: 题型:
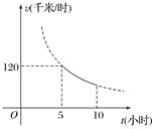
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明在一次打篮球时,篮球传出后的运动路线为如图所示的抛物线,以小明所站立的位置为原点O建立平面直角坐标系,篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=-![]() x2+x+c.
x2+x+c.
(1)求y与x之间的函数表达式;
(2)球在运动的过程中离地面的最大高度;
(3)小亮手举过头顶,跳起后的最大高度为BC=2.5m,若小亮要在篮球下落过程中接到球,求小亮离小明的最短距离OB.

查看答案和解析>>
科目: 来源: 题型:
【题目】某公司计划投入50万元,开发并生产甲乙两种产品,根据市场调查预计甲产品的年获利y1(万元)与投入资金x(万元)成正比例,乙产品的年获利y2(万元)与投入资金x(万元)的平方成正比例,设该公司投入乙产品x(万元),两种产品的年总获利为y万元(x≥0),得到了表中的数据.
x(万元) | 20 | 30 |
y(万元) | 10 | 13 |
(1)求y与x的函数关系式;
(2)该公司至少可获得多少利润?请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议,使他能获得最大利润,并求出最大利润是多少?
(3)若从年总利润扣除投入乙产品资金的a倍(a≤1)后,剩余利润随x增大而减小,求a的取值
范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】例 如图①,李老师设计了一个探究杠杆平衡条件的实验:在一个自制的类似天平的仪器的左边固定托盘![]() 中放置一个重物,在右边活动托盘
中放置一个重物,在右边活动托盘![]() (可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘
(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘![]() 与点
与点![]() 的距离
的距离![]() ,观察活动托盘
,观察活动托盘![]() 中砝码的质量
中砝码的质量![]() 的变化情况.实验数据记录如表:
的变化情况.实验数据记录如表:
| 10 | 15 | 20 | 25 | 30 |
| 30 | 20 | 15 | 12 | 10 |
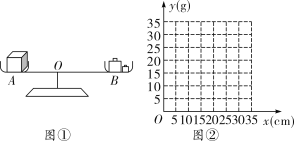
(1)把表中![]() 的各组对应值作为点的坐标,在图②的坐标系中描出相应的点,用平滑曲线连接这些点;
的各组对应值作为点的坐标,在图②的坐标系中描出相应的点,用平滑曲线连接这些点;
(2)观察所画的图象,猜测![]() 与
与![]() 之间的函数关系,求出函数关系式;
之间的函数关系,求出函数关系式;
(3)当砝码的质量为![]() 时,活动托盘
时,活动托盘![]() 与点
与点![]() 的距离是多少?
的距离是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校准备组织师生共60人,从甲地乘动车前往乙地参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
甲地 | 乙地 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)求参加活动的教师和学生各有多少人?
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,后续前往的教师和学生均购买二等座票.设提早前往的教师有![]() 人,购买一、二等座票全部费用为
人,购买一、二等座票全部费用为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若购买一、二等座票全部费用不多于1030元,则提早前往的教师最多只能有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用![]() (元)随时间
(元)随时间![]() (天)的变化图象为折线
(天)的变化图象为折线![]() ,如图所示.
,如图所示.
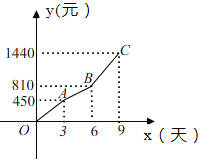
(1)当租赁时间不超过3天时,求每日租金.
(2)当![]() 时,求
时,求![]() (元)与
(元)与![]() (天)的函数关系式.
(天)的函数关系式.
(3)甲、乙两人租赁该款汽车各一辆,两人租赁的时间共为9天,甲租的天数少于3天,乙比甲多支付费用720元.请问乙租这款汽车多长时间?
查看答案和解析>>
科目: 来源: 题型:
【题目】在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为x,y.
①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】某新建小区要修一条1050米长的路,甲、乙两个工程队想承建这项工程.经
了解得到以下信息(如表):
工程队 | 每天修路的长度(米) | 单独完成所需天数(天) | 每天所需费用(元) |
甲队 | 30 | n | 600 |
乙队 | m | n﹣14 | 1160 |
(1)甲队单独完成这项工程所需天数n= ,乙队每天修路的长度m= (米);
(2)甲队先修了x米之后,甲、乙两队一起修路,又用了y天完成这项工程(其中x,y为正整数).
①当x=90时,求出乙队修路的天数;
②求y与x之间的函数关系式(不用写出x的取值范围);
③若总费用不超过22800元,求甲队至少先修了多少米.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() ,
,![]() 两地相距
两地相距![]() .甲、乙两人都由
.甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]() .
.
(1)根据题意,填写下表:
时间 与 | 0.5 | 1.8 | ______ |
甲与 | 5 | ______ | 20 |
乙与 | 0 | 12 | ______ |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() ,写出
,写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com