
科目: 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在平面直角坐标系xOy中,直线l1分别交x轴和y轴于点A(﹣3,0),B(0,3).
(1)如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;
(2)如图2,已知直线l2:y=3x﹣3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,2![]() 为半径画圆.
为半径画圆.
①当点Q与点C重合时,求证:直线l1与⊙Q相切;
②设⊙Q与直线l1相交于M,N两点,连结QM,QN.问:是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
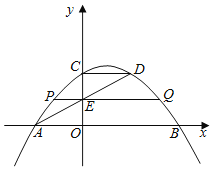
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+2与x轴相交于A、B两点,与y轴相交于点C,点D在抛物线上,且CD∥AB.AD与y轴相交于点E,过点E的直线PQ平行于x轴,与拋物线相交于P,Q两点,则线段PQ的长为_____.
x+2与x轴相交于A、B两点,与y轴相交于点C,点D在抛物线上,且CD∥AB.AD与y轴相交于点E,过点E的直线PQ平行于x轴,与拋物线相交于P,Q两点,则线段PQ的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的材料:
如果函数![]() 满足:对于自变量
满足:对于自变量![]() 的取值范围内的任意
的取值范围内的任意![]() ,
,![]() ,
,
(1)若![]() ,都有
,都有![]() ,则称
,则称![]() 是增函数;
是增函数;
(2)若![]() ,都有
,都有![]() ,则称
,则称![]() 是减函数.
是减函数.
例题:证明函数![]() 是减函数.
是减函数.
证明:设![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .即
.即![]() .
.
∴![]() .
.
∴函数![]() 是减函数.
是减函数.
根据以上材料,解答下面的问题:
已知函数![]() ,
,
![]() ,
,![]()
(1)计算:![]() ,
,![]() ;
;
(2)猜想:函数![]() 是 函数(填“增”或“减”);
是 函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
科目: 来源: 题型:
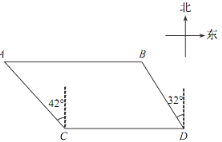
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
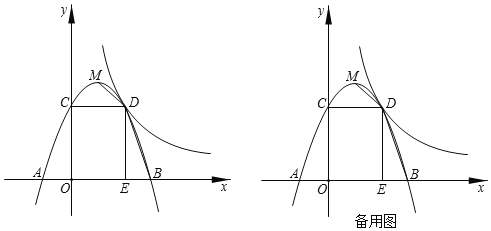
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C,过点C作CD⊥y轴交抛物线于另一点D,作DE⊥x轴,垂足为点E,双曲线y=![]() (x>0)经过点D,连接MD,BD.
(x>0)经过点D,连接MD,BD.
(1)求抛物线的表达式;
(2)点N,F分别是x轴,y轴上的两点,当以M,D,N,F为顶点的四边形周长最小时,求出点N,F的坐标;
(3)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?
查看答案和解析>>
科目: 来源: 题型:
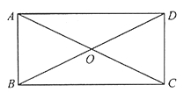
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某球室有三种品牌的![]() 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知
个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知![]() (一次拿到
(一次拿到![]() 元球)
元球)![]() .
.
(1)求这![]() 个球价格的众数;
个球价格的众数;
(2)若甲组已拿走一个![]() 元球训练,乙组准备从剩余
元球训练,乙组准备从剩余![]() 个球中随机拿一个训练.
个球中随机拿一个训练.
①所剩的![]() 个球价格的中位数与原来
个球价格的中位数与原来![]() 个球价格的中位数是否相同?并简要说明理由;
个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿 先拿 | |||
查看答案和解析>>
科目: 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com