
科目: 来源: 题型:
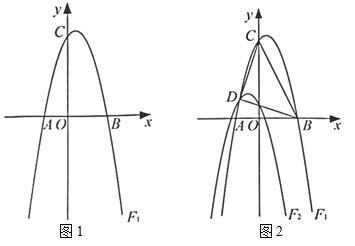
【题目】如图1所示,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)如图2,将抛物线![]() 先向左平移1个单位,再向下平移3个单位,得到抛物线
先向左平移1个单位,再向下平移3个单位,得到抛物线![]() ,若抛物线
,若抛物线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①求点![]() 的坐标;
的坐标;
②判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)在(2)的条件下,抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,动点
,动点![]() ,
,![]() 分别从
分别从![]() 点,
点,![]() 点同时以每秒1个单位长度的速度出发,且分别在边
点同时以每秒1个单位长度的速度出发,且分别在边![]() 上沿
上沿![]() ,
,![]() 的方向运动,当点
的方向运动,当点![]() 运动到点
运动到点![]() 时,
时,![]() 两点同时停止运动,设点
两点同时停止运动,设点![]() 运动的时间为
运动的时间为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
(1)如图2,当![]() 时,延长
时,延长![]() 交边
交边![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)在(1)的条件下,试探究线段![]() 三者之间的等量关系,并加以证明;
三者之间的等量关系,并加以证明;
(3)如图3,当![]() 时,延长
时,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如下两幅不完整的统计图:
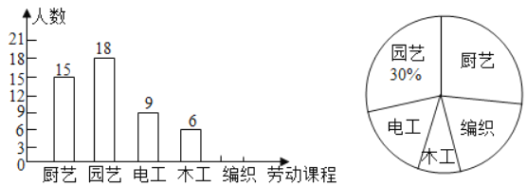
(1)本次随机调查的学生人数为 人;
(2)补全条形统计图;
(3)若该校七年级共有800名学生,请估计该校七年级学生选择“厨艺”劳动课程的人数;
(4)七(1)班计划在“园艺、电工、木工、编织”四大类劳动课程中任选两类参加学校期末展示活动,请用列表或画树状图的方法,求恰好选中“园艺、编织”这两类劳动课程的概率.
查看答案和解析>>
科目: 来源: 题型:
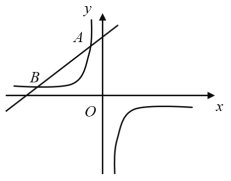
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象相交于
)的图象相交于![]() ,
,![]() 两点.
两点.
(1)求反比例函数的表达式;
(2)将一次函数![]() 的图象沿
的图象沿![]() 轴向下平移
轴向下平移![]() 个单位
个单位![]() ,使平移后的图象与反比例函数
,使平移后的图象与反比例函数![]() 的图象有且只有一个交点,求
的图象有且只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
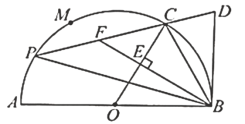
【题目】如图,![]() 为半⊙O的直径,
为半⊙O的直径,![]() ,
,![]() 是半圆上的三等分点,
是半圆上的三等分点,![]() ,
,![]() 与半⊙O相切于点
与半⊙O相切于点![]() ,点
,点![]() 为
为![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),直线
重合),直线![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则下列结论正确的是______________.(写出所有正确结论的序号)
,则下列结论正确的是______________.(写出所有正确结论的序号)
①![]() ;②
;②![]() 的长为
的长为![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,抛物线![]() 与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
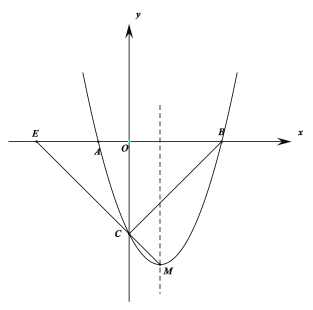
(1)求点C及顶点M的坐标.
(2)若点N是第四象限内抛物线上的一个动点,连接![]() 求
求![]() 面积的最大值及此时点N的坐标.
面积的最大值及此时点N的坐标.
(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(4)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与![]() 相似.若存在,求出点P的坐标;若不存在,请说明理由.
相似.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在⊙O中,AB为直径,点C为圆上一点,延长AB到点D,使CD=CA,且![]() .
.

(1)求证:![]() 是⊙O的切线.
是⊙O的切线.
(2)分别过A、B两点作直线CD的垂线,垂足分别为E、F两点,过C点作AB的垂线,垂足为点G.求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店计划采购甲、乙两种不同型号的平板电脑共20台,已知甲型平板电脑进价1600元,售价2000元;乙型平板电脑进价为2500元,售价3000元.
(1)设该商店购进甲型平板电脑x台,请写出全部售出后该商店获利y与x之间函数表达式.
(2)若该商店采购两种平板电脑的总费用不超过39200元,全部售出所获利润不低于8500元,请设计出所有采购方案,并求出使商店获得最大利润的采购方案及最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是____________(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,过点D作BD垂线交BC的延长线于点E,且
,过点D作BD垂线交BC的延长线于点E,且![]() ,证明:四边形
,证明:四边形![]() 是垂等四边形.
是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形![]() 内接于⊙O中,
内接于⊙O中,![]() .求⊙O的半径.
.求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com