
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
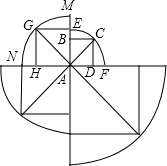 法依次进行到如图所示,叫做正方形ABCD面积的第一次扩展.按这种方法可进行第二次扩展,直到第n次扩展
法依次进行到如图所示,叫做正方形ABCD面积的第一次扩展.按这种方法可进行第二次扩展,直到第n次扩展查看答案和解析>>
科目: 来源: 题型:
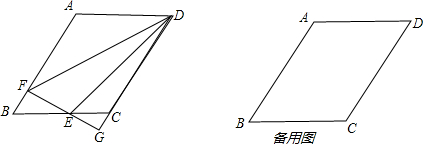
 如图1,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.则有结论EF=BE+FD成立;
如图1,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.则有结论EF=BE+FD成立;查看答案和解析>>
科目: 来源: 题型:
| 温度(℃) | -6 | -4 | -2 | 0 | 2 | 4 |
| 植物高度的增长量(mm) | 25 | 41 | 49 | 49 | 41 | 25 |
| k |
| x |
查看答案和解析>>
科目: 来源: 题型:
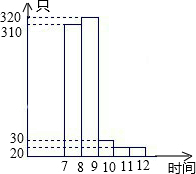 况,下面是第二候鸟监测站在3月28日监测到上空飞过候鸟数的直方图:
况,下面是第二候鸟监测站在3月28日监测到上空飞过候鸟数的直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com