
科目: 来源: 题型:
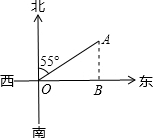 如图,灯塔A在港口O的北偏东55°方向上,且与港口的距离为80海里,一艘船上午9时从港口O出发向正东方向航行,上午11时到达B处,看到灯塔A在它的正北方向.试求这艘船航行的速度.(精确到0.01海里/小时)(供选用数据:sin55°=0.8192,cos55°=0.5736,tan55°=1.4281)
如图,灯塔A在港口O的北偏东55°方向上,且与港口的距离为80海里,一艘船上午9时从港口O出发向正东方向航行,上午11时到达B处,看到灯塔A在它的正北方向.试求这艘船航行的速度.(精确到0.01海里/小时)(供选用数据:sin55°=0.8192,cos55°=0.5736,tan55°=1.4281)查看答案和解析>>
科目: 来源: 题型:
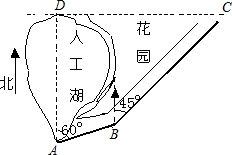 初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图A、D是人工湖边的两座雕塑,AB、BC是湖滨花园的小路,小东同学进行如下测量,B点在A点北偏东60°方向,C点在B点北偏东45°方向,C点在D点正东方向,且测得AB=20米,BC=40米,求AD的长.(
初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图A、D是人工湖边的两座雕塑,AB、BC是湖滨花园的小路,小东同学进行如下测量,B点在A点北偏东60°方向,C点在B点北偏东45°方向,C点在D点正东方向,且测得AB=20米,BC=40米,求AD的长.(| 3 |
| 2 |
查看答案和解析>>
科目: 来源: 题型:
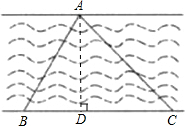 为了测量汉江某段河面的宽度,秋实同学设计了如下图所示的测量方案:先在河的北岸选一定点A,再在河的南岸选定相距a米的两点B、C(如图),分别测得∠ABC=α,∠ACB=β,请你根据秋实同学测得的数据,计算出河宽AD.(结果用含a和含α、β的三角函数表示)
为了测量汉江某段河面的宽度,秋实同学设计了如下图所示的测量方案:先在河的北岸选一定点A,再在河的南岸选定相距a米的两点B、C(如图),分别测得∠ABC=α,∠ACB=β,请你根据秋实同学测得的数据,计算出河宽AD.(结果用含a和含α、β的三角函数表示)查看答案和解析>>
科目: 来源: 题型:
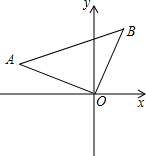 ,1).
,1).查看答案和解析>>
科目: 来源: 题型:
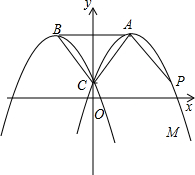 点C;抛物线N与抛物线M关于y轴对称,其顶点为B,连接AC,BC,AB.
点C;抛物线N与抛物线M关于y轴对称,其顶点为B,连接AC,BC,AB.查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
| ||
| 3 |
| ||
| 2 |
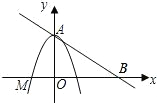 四边形是平行四边形.
四边形是平行四边形.查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
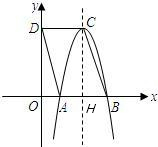
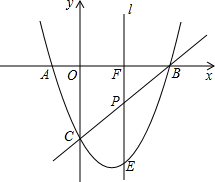 点C.点P为线段BC上一点,过点P作直线l⊥x轴于点F,交抛物线c1点E.
点C.点P为线段BC上一点,过点P作直线l⊥x轴于点F,交抛物线c1点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com