
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
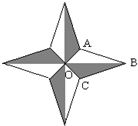 8、如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四边形OABC绕点O进行3次旋转变换后形成的.测得AB=BC,OA=OC,∠ABC=40°,则∠OAB的度数是( )
8、如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四边形OABC绕点O进行3次旋转变换后形成的.测得AB=BC,OA=OC,∠ABC=40°,则∠OAB的度数是( )查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
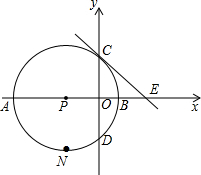 已知A(-3,0)、B(1,0),过点C作⊙P的切线交x轴于点E.
已知A(-3,0)、B(1,0),过点C作⊙P的切线交x轴于点E. | ADB |
查看答案和解析>>
科目: 来源: 题型:
| ||
| 3 |
| ||
| 3 |
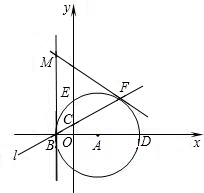 (1)直接写出点B、C的坐标;
(1)直接写出点B、C的坐标; |
| BEF |
 |
| BEF |
查看答案和解析>>
科目: 来源: 题型:
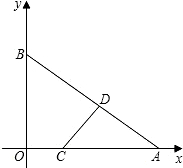 取值范围:若不可能,请说明理由.
取值范围:若不可能,请说明理由.查看答案和解析>>
科目: 来源: 题型:
| ||
| 2 |
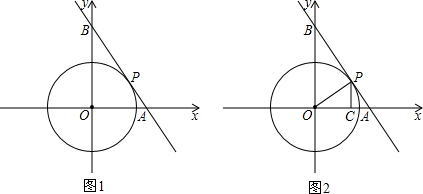
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:| 指距d(cm) | 20 | 21 | 22 | 23 |
| 身高h(cm) | 160 | 169 | 178 | 187 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com