
科目: 来源: 题型:
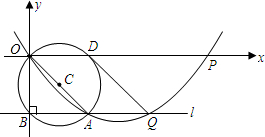
查看答案和解析>>
科目: 来源: 题型:
| 24 | x |
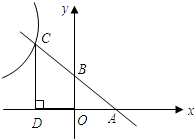 明理由.
明理由.查看答案和解析>>
科目: 来源: 题型:
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
查看答案和解析>>
科目: 来源: 题型:

查看答案和解析>>
科目: 来源: 题型:
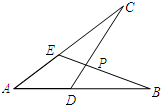 ②AB=AC;③BE=CD.
②AB=AC;③BE=CD.查看答案和解析>>
科目: 来源: 题型:
 22、在由四个相同的小正方形组成的“7”字形图中,请你添画一个小正方形,使它成为轴对称图形,并用虚线画出它的对称轴.要求在图(1)、图(2)、图(3)中画出三种不同的设计图案(不要求尺规作图).
22、在由四个相同的小正方形组成的“7”字形图中,请你添画一个小正方形,使它成为轴对称图形,并用虚线画出它的对称轴.要求在图(1)、图(2)、图(3)中画出三种不同的设计图案(不要求尺规作图).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com