有一横截面积为1600厘米2的圆筒形容器,内有20千克的水,将一个40×30×20厘米3的木块竖直放入容器底,ρ木=O.6克/厘米3,水未溢出:求木块所受浮力和木块对容器底的压强?
【答案】
分析:(1)知道木块的密度,求出木块的体积,利用密度公式求木块的质量,再利用重力公式求木块重;
假设木块恰能漂浮,根据漂浮条件求受到的浮力,再利用阿基米德原理求排开水的体积,进而求出将木块竖直浸入水中能浮起来时浸入的深度;
知道水的质量,利用密度公式求水的体积,加上排开水的体积,可求容器内水的深度,和将木块竖直浸入水中能浮起来时浸入的深度比较得出木块能否浮起来;
(2)若不能浮起来,设木块浸入的深度(水深)为h,则木块排开水的体积加上水的体积等于容器底面积乘以h,据此出浸入深度h,进而求出木块排开水的体积,利用阿基米德原理求木块受到的浮力;
(3)木块对容器底的压力等于木块重减去浮力,利用压强公式求木块对容器底的压强.
解答:解:
(1)木块重:
G=mg=ρ
木Vg=O.6×10
3kg/m
3×40×30×20×10
-6m
3×10N/kg=144N,
若木块漂浮,则
F
浮=G=144N,
∵F
浮=ρ
水V
排g,
∴V
排=
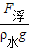
=
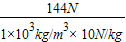
=0.0144m
3,
木块竖直浸入的深度:
h
浸=
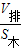
=
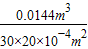
=0.24m,
水的体积:
V
水=
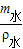
=
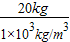
=0.02m
3,
放入木块后的水深:
h
水=
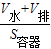
=
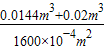
=0.215m,
∵h
浸>h
水,
∴木块在水中不能浮起来;
(2)由上面的分析可知,木块不能浮起来,设木块浸入的深度(水深)为h,则S
容器h=V
排+V
水=S
木h+V
水,
即:1600×10
-4m
2×h=30×20×10
-4m
2×h+0.02m
3,
解得:
h=0.2m,
木块排开水的体积:
V
排=S
木h=30×20×10
-4m
2×0.2m=0.012m
3,
木块受到的浮力:
F
浮=ρ
水V
排g=1×10
3kg/m
3×0.012m
3×10N/kg=120N;
(3)木块对容器底的压力:
F
压=G-F
浮=144N-120N=24N,
木块对容器底的压强:
p=
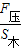
=
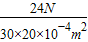
=400Pa.
答:木块所受浮力为120N,木块对容器底的压强为400Pa.
点评:本题为力学综合题,考查了学生对重力公式、密度公式、阿基米德原理、物体的漂浮条件、压强公式的掌握和运用,能判断木块在水中不能浮起来是本题的关键.

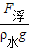 =
=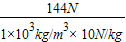 =0.0144m3,
=0.0144m3,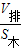 =
=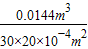 =0.24m,
=0.24m,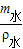 =
=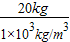 =0.02m3,
=0.02m3,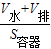 =
=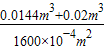 =0.215m,
=0.215m,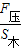 =
=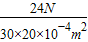 =400Pa.
=400Pa.
