
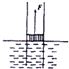
 如图所示,在河中间固定一个细长圆管,管内有一轻质活塞,活塞下端位于水面,面积为1厘米2,质量不计,大气压强为1.0×105帕.现将活塞缓慢提高15米,则在该过程中外力对活塞做功为
如图所示,在河中间固定一个细长圆管,管内有一轻质活塞,活塞下端位于水面,面积为1厘米2,质量不计,大气压强为1.0×105帕.现将活塞缓慢提高15米,则在该过程中外力对活塞做功为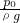 =
= =10m.
=10m. ρgh1S.
ρgh1S. ρgh1S?h1=
ρgh1S?h1= ×1.0×103kg/m3×10N/kg×10m×1×10-4m2×10m=50J.
×1.0×103kg/m3×10N/kg×10m×1×10-4m2×10m=50J.

科目:初中物理 来源: 题型:
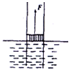 如图所示,在河中间固定一个细长圆管,管内有一轻质活塞,活塞下端位于水面,面积为1厘米2,质量不计,大气压强为1.0×105帕.现将活塞缓慢提高15米,则在该过程中外力对活塞做功为( )
如图所示,在河中间固定一个细长圆管,管内有一轻质活塞,活塞下端位于水面,面积为1厘米2,质量不计,大气压强为1.0×105帕.现将活塞缓慢提高15米,则在该过程中外力对活塞做功为( )查看答案和解析>>
科目:初中物理 来源: 题型:
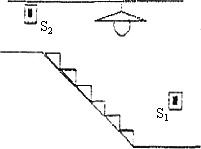 如图所示,在楼道中间安装的电灯,需要在楼梯的上下两头都能控制它,当人上楼梯时,能用下面的开关S1开灯,人上了楼梯以后,能用上面的开关S2关灯;当下楼梯时,能用S2开灯,用S1关灯,请画出电路图.
如图所示,在楼道中间安装的电灯,需要在楼梯的上下两头都能控制它,当人上楼梯时,能用下面的开关S1开灯,人上了楼梯以后,能用上面的开关S2关灯;当下楼梯时,能用S2开灯,用S1关灯,请画出电路图.查看答案和解析>>
科目:初中物理 来源:2005-2006学年北师大版九年级(上)期中物理试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中物理 来源:2007年上海市第二十一届初中物理竞赛初赛试卷(大同中学杯)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com