
 (1)某班级组织了一次物理课外实践活动,试比较全班同学中从一楼爬上三楼过程中谁的爬楼功率最大.为了简便获得比赛结果,则活动中至少测量的物理量是:人体的体重和________.实验结束后,有位质量为50kg同学进行爬杆训练,当他沿竖直杆匀速上爬时,人受到的摩擦力大小为________ N,方向________(g=10N/kg).
(1)某班级组织了一次物理课外实践活动,试比较全班同学中从一楼爬上三楼过程中谁的爬楼功率最大.为了简便获得比赛结果,则活动中至少测量的物理量是:人体的体重和________.实验结束后,有位质量为50kg同学进行爬杆训练,当他沿竖直杆匀速上爬时,人受到的摩擦力大小为________ N,方向________(g=10N/kg). =10kg,所以一次搬运3箱;
=10kg,所以一次搬运3箱;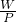 =
=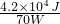 =600s.
=600s.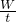 比较上楼的功率大小关系;先根据G=mg求出小宇的重力,然后对小宇进行受力分析,再根据小宇匀速下滑,受到平衡力作用,根据二力平衡的条件求出摩擦力的大小.
比较上楼的功率大小关系;先根据G=mg求出小宇的重力,然后对小宇进行受力分析,再根据小宇匀速下滑,受到平衡力作用,根据二力平衡的条件求出摩擦力的大小.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中物理 来源: 题型:
 (2010?白下区二模)(1)某班级组织了一次物理课外实践活动,试比较全班同学中从一楼爬上三楼过程中谁的爬楼功率最大.为了简便获得比赛结果,则活动中至少测量的物理量是:人体的体重和
(2010?白下区二模)(1)某班级组织了一次物理课外实践活动,试比较全班同学中从一楼爬上三楼过程中谁的爬楼功率最大.为了简便获得比赛结果,则活动中至少测量的物理量是:人体的体重和查看答案和解析>>
科目:初中物理 来源:江苏模拟题 题型:填空题

查看答案和解析>>
科目:初中物理 来源:2010年江苏省南京市白下区中考物理二模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com