
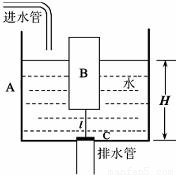
 某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口.浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L.当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开.问
某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口.浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L.当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开.问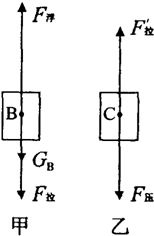 解:由题知:H=60cm;mB=0.2kg;S1=80cm2;hB=30cm;S2=40cm2;d=1cm;
解:由题知:H=60cm;mB=0.2kg;S1=80cm2;hB=30cm;S2=40cm2;d=1cm;


科目:初中物理 来源: 题型:
 某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个边长为50cm的正方体;浮筒B是一个质量为0.2kg的空心圆柱体,其底面积SB为80cm2,高为35cm;放水阀门C是一个质量可忽略的圆柱体,其底面积Sc为55cm2,厚度d为1.5cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻绳与浮筒相连,绳的长度l为10cm.请你计算出水箱中的水深H至少为多少时,浮筒B刚好能将放水阀门C打开?
某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个边长为50cm的正方体;浮筒B是一个质量为0.2kg的空心圆柱体,其底面积SB为80cm2,高为35cm;放水阀门C是一个质量可忽略的圆柱体,其底面积Sc为55cm2,厚度d为1.5cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻绳与浮筒相连,绳的长度l为10cm.请你计算出水箱中的水深H至少为多少时,浮筒B刚好能将放水阀门C打开?查看答案和解析>>
科目:初中物理 来源: 题型:
 某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口.浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L.当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开.问
某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物.如图是这种水箱模型的主要部件的截面示意图.图中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口.浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L.当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开.问查看答案和解析>>
科目:初中物理 来源:2013年名校初升高自主招生物理综合练习卷(三)(解析版) 题型:解答题
查看答案和解析>>
科目:初中物理 来源:2010年中考物理能力测试试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com