Question

一束光线与平面镜成50°角入射，则反射光线与入射光线的夹角为    ，若入射光线不变，平面镜转过20°，反射光线转过    ．
若两个平面镜M、N之间的夹角为θ，入射光线与镜面M平行，经过两个平面镜反射后，反射光线与镜面N平行，则θ的大小为    °．

Answer 1

【答案】分析：（1）入射光线与法线间的夹角是入射角，反射光线间的夹角是反射角；
光的反射定律：入射光线、法线、反射光线在同一个平面内；
入射光线与反射光线位于法线的两侧，反射角等于入射角．
（2）反射两次后平行与OA，做出光的反射光路图，根据光路图可以确定两平面镜之间的夹角α．
解答：解：（1）①入射光线与镜面的夹角为50°，入射角为90°-50°=40°，
由反射定律可知：反射角等于入射角也等于40°；
则入射光线与反射光线间的夹角40°+40°=80°．
②入射光线不变，平面镜转过20°，入射角改变20°，
由光反射定律可知，反射角等于入射角，反射角也改变20°，
则反射光线转过的角度是20°+20°=40°．
（2）作出光的反射光路图如右图所示，
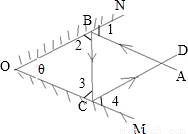
入射光跟平面镜OM平行，出射光跟ON平行，如图所示，
AB∥OM，CD∥ON，则∠1=θ，∠4=θ．
由光的反射定律可知，反射角等于入射角，
所以∠2=∠1=θ，∠3=∠4=θ，
所以△BOC为等边三角形，所以θ=60°．
故答案为：80°；40°；60．
点评：（1）本题主要考查的是光的反射定律的应用，以及利用反射定律对反射角和入射角进行计算，只要熟记反射定律的内容，怎么旋转镜面也不怕．
（2）此题主要考查了光的反射定律，结合平行线的性质和反射，最后利用三角形的内角和求解，此题体现了不同学科间是相互联系的特点．