在古代人们将漂浮在水面上的树干挖空成为独木舟.在实验室中同学们利用长0.4m、宽0.2m、高0.1m的长方体木块进行研究,木块密度是0.6×103Kg/m3.求:
(1)当木块漂浮在水面上时,它露出水面部分的体积是多少?
(2)若将木块中间挖空,使空心部分的体积为5×10-3m3,将木块做成一只“小船”,这只小船最多能装载多少货物?(g=10N/Kg ρ水=1.0×103Kg/m3)
解:(1)V
木=0.4m×0.2m×0.1m=8×10
-3m
3G
木=mg=ρ
木V
木g=0.6×10
3Kg/m
3×8×10
-3m
3×10N/Kg
=48N(1分)
木块漂浮在水面G
木=F
浮=48N(1分)
F
浮=ρ
液gv
排(1分)
V
排=
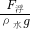
=

=4.8×10
-3m
3(1分)
V
外=V
木-V
排=8×10
-3m
3-4.8×10
-3m
3=3.2×10
-3m
3(1分)
(2)V
船=V
木-V
空=8×10
-3m
3-5×10
-3m
3=3×10
-3m
3G
船=m
船g=ρ
木V
船g=0.6×10
3Kg/m
3×3×10
-3m
3×10N/Kg=18N(1分)
船漂浮时最大浮力F
浮最大=ρ
水gv
木=1.0×10
3Kg/m
3×10N/Kg×8×10
-3m
3=80N(1分)
船漂浮G
物=F
浮最大-G
船=80N-18N=62N(1分)
答:(1)当木块漂浮在水面上时露出水面部分的体积是3.2×10
-3m
3;
(2)这只小船最多能装载货物62N.
分析:(1)先求出长方体木块的体积,再求出木块的重力,根据漂浮时F
浮=G
木,再根据浮力公式变形即可求得V
排,再用总体积减去没入水中的体积即为露出水面部分的体积.
(2)先求出小船的体积,再求船的重力,再求船漂浮时最大浮力,那么这只小船最多能装载的货物就是船的最大浮力减去船的重力.
点评:此题主要考查学生的知识点较多,有浮力大小的计算、密度公式的应用、物体的浮沉条件及其应用,尤其是公式变形的情况较多,步骤繁琐,是一道难题.

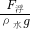 =
= =4.8×10-3m3(1分)
=4.8×10-3m3(1分)

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案