
 如图所示,容器底部一根中间为圆柱形的管子与大气相连,管的直径为20cm,不计管壁的厚度.现在管子上方压一个边长为50cm的塑胶立方体,将管口封住.使容器中盛有一定质量的水.已知大气压强为1.0×105Pa.塑胶立方体的密度为0.6×103kg/m3.当水面恰好在塑胶方立体高的中点时.塑胶立方体受到水对它的浮力大小为________N.当容器中所盛水的水面到塑胶立方体底面的高度满足一定的条件时,塑胶立方体能封住管口,不让水从管子的孔中流水.该条件是________.(计算时保留小数点后两位)
如图所示,容器底部一根中间为圆柱形的管子与大气相连,管的直径为20cm,不计管壁的厚度.现在管子上方压一个边长为50cm的塑胶立方体,将管口封住.使容器中盛有一定质量的水.已知大气压强为1.0×105Pa.塑胶立方体的密度为0.6×103kg/m3.当水面恰好在塑胶方立体高的中点时.塑胶立方体受到水对它的浮力大小为________N.当容器中所盛水的水面到塑胶立方体底面的高度满足一定的条件时,塑胶立方体能封住管口,不让水从管子的孔中流水.该条件是________.(计算时保留小数点后两位)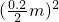 =0.2186m2.
=0.2186m2.

科目:初中物理 来源: 题型:
 如图所示,容器底部用一根细绳拉住一木球,使木球全部浸入水中,已知木球的密度是水的密度的
如图所示,容器底部用一根细绳拉住一木球,使木球全部浸入水中,已知木球的密度是水的密度的| 3 | 5 |
查看答案和解析>>
科目:初中物理 来源: 题型:
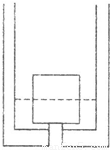
 如图所示,容器底部一根中间为圆柱形的管子与大气相连,管的直径为20cm,不计管壁的厚度.现在管子上方压一个边长为50cm的塑胶立方体,将管口封住.使容器中盛有一定质量的水.已知大气压强为1.O×105Pa.塑胶立方体的密度为O.6×lO3kg/m3.当水面恰好在塑胶方立体高的中点时.塑胶立方体受到水对它的浮力大小为
如图所示,容器底部一根中间为圆柱形的管子与大气相连,管的直径为20cm,不计管壁的厚度.现在管子上方压一个边长为50cm的塑胶立方体,将管口封住.使容器中盛有一定质量的水.已知大气压强为1.O×105Pa.塑胶立方体的密度为O.6×lO3kg/m3.当水面恰好在塑胶方立体高的中点时.塑胶立方体受到水对它的浮力大小为查看答案和解析>>
科目:初中物理 来源:2005年上海市第十九届初中物理竞赛复赛试卷(大同中学杯)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com