
| A. | 配制前,这两种液体的原体积相等 | |
| B. | 这种混合液的密度为$\frac{{ρ}_{1}+{ρ}_{2}}{2}$ | |
| C. | 所得混合液的质量最大为(1+$\frac{{ρ}_{2}}{{ρ}_{1}}$)m0 | |
| D. | 按要求配制后,剩下的那部分液体的质量为(1-$\frac{{ρ}_{1}}{{ρ}_{2}}$)m0 |
分析 要当两种液体的体积相等时,我们可设每种液体的体积为V,则混合液体的体积为2V,然后根据公式m=ρV得出这两种液体的质量表达式,从而就可以得出混合液体的质量表达式,最后根据密度公式得出混合液体的密度表达式.
解答 解:A、已知配制前两种液体质量相等,由体积公式V=$\frac{m}{ρ}$可知,质量相同,密度不等,故体积不相等,故A错误;
B、设所需液体的体积为V,则混合液体的总体积为2V,
两种液体的质量分别为m1=ρ1V,m2=ρ2V,则混合液体的总质量为m=m1+m2=ρ1V+ρ2V,
所以,混合液体的密度为ρ=$\frac{m}{2V}$=$\frac{{ρ}_{1}V+{ρ}_{2}V}{2V}$=$\frac{{ρ}_{1}+{ρ}_{2}}{2}$,故B正确;
C、因为原来两液体的质量相等,且ρ1<ρ2,
所以,由V=$\frac{m}{ρ}$可知,V1>V2,即质量相等的两液体,密度为ρ1的液体体积较大;
因为要用它们按体积比1:1的比例配制,当V2已用完、V1有剩余时,即两种液体所取的体积均为V2时(其中V2=$\frac{{m}_{0}}{{ρ}_{2}}$),所得混合液的质量最大;
故混合液的最大质量:
m最大=m0+m1′=m0+ρ1V1′=m0+ρ1V2=m0+ρ1$\frac{{m}_{0}}{{ρ}_{2}}$=(1+$\frac{{ρ}_{1}}{{ρ}_{2}}$)m0,故C错误;
则剩下的那部分液体的质量为:m剩=m0-ρ1V2=m0-ρ1$\frac{{m}_{0}}{{ρ}_{2}}$=(1-$\frac{{ρ}_{1}}{{ρ}_{2}}$)m0,故D正确.
故选BD.
点评 本题考查了有关混合液密度的计算,关键是知道两液体等质量混合时混合液的密度、等体积混合时混合液的密度,是道难题.


科目:初中物理 来源: 题型:实验探究题
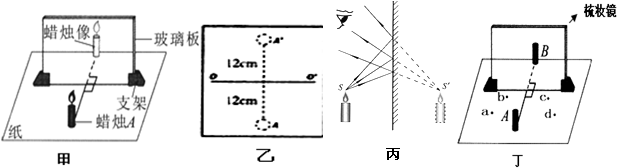
查看答案和解析>>
科目:初中物理 来源: 题型:实验探究题
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
 如图所示,锤子的锤头变松了,人们常用撞击锤柄下端的方法使锤头紧套在锤柄上.这是因为锤柄下端受到撞击时,锤柄先停止运动,利用锤头的惯性,使锤头套紧锤柄且锤头质量越大越容易套紧.
如图所示,锤子的锤头变松了,人们常用撞击锤柄下端的方法使锤头紧套在锤柄上.这是因为锤柄下端受到撞击时,锤柄先停止运动,利用锤头的惯性,使锤头套紧锤柄且锤头质量越大越容易套紧.查看答案和解析>>
科目:初中物理 来源: 题型:填空题
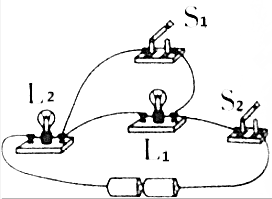
查看答案和解析>>
科目:初中物理 来源: 题型:计算题
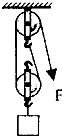 如图所示,用滑轮组把重为80N的物体匀速提起,试计算:
如图所示,用滑轮组把重为80N的物体匀速提起,试计算:查看答案和解析>>
科目:初中物理 来源: 题型:解答题
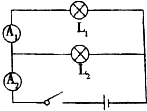 如图所示.开关闭合后两灯泡L1、L2均发光,电流表A1、A2读数分别为0.6A、0.9A.
如图所示.开关闭合后两灯泡L1、L2均发光,电流表A1、A2读数分别为0.6A、0.9A.查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com