
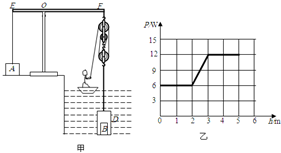
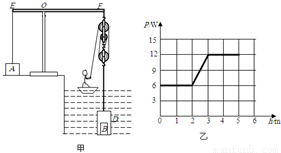
 如图甲所示是一个装置示意图,正方体A作为配重使用,保证杠杆EOF始终在水平位置平衡.某同学用这个装置和一个圆柱形密闭容器D提取水中的圆柱体B;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率和密闭容器D匀速被提升的距离关系如图22乙所示;在提升全过程中,密闭容器D上升速度始终保持不变,配重A始终没有离开地面,每个滑轮的质量都相等.已知密闭容器D的底面积为SD=1.2×10-2m2,质量为mD=3kg;正方体A单独放在水平地面上,对地面的压强为p0=3×104Pa,密闭容器D未被提出水面匀速上升和完全提出水面后匀速上升,A对地面的压强分别为p1=2.1×104 Pa,p2=1.3×104 Pa.(不计绳的重力,滑轮与轴的摩擦及水的阻力,不考虑水面高度变化,g取10N/kg)
如图甲所示是一个装置示意图,正方体A作为配重使用,保证杠杆EOF始终在水平位置平衡.某同学用这个装置和一个圆柱形密闭容器D提取水中的圆柱体B;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率和密闭容器D匀速被提升的距离关系如图22乙所示;在提升全过程中,密闭容器D上升速度始终保持不变,配重A始终没有离开地面,每个滑轮的质量都相等.已知密闭容器D的底面积为SD=1.2×10-2m2,质量为mD=3kg;正方体A单独放在水平地面上,对地面的压强为p0=3×104Pa,密闭容器D未被提出水面匀速上升和完全提出水面后匀速上升,A对地面的压强分别为p1=2.1×104 Pa,p2=1.3×104 Pa.(不计绳的重力,滑轮与轴的摩擦及水的阻力,不考虑水面高度变化,g取10N/kg) =
=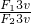 =
= =
=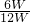 =
= ,
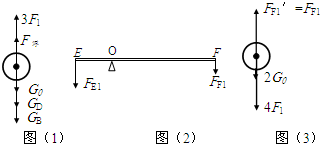
,

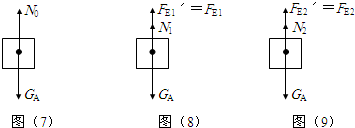
 =
= ,F浮=120N及上式可得:F1=40N,F2=80N;
,F浮=120N及上式可得:F1=40N,F2=80N;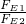 =
= ,
,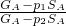 =
=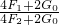
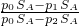 =
=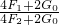
 ×100%=
×100%=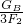 ×100%=
×100%=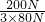 ×100%=83%.
×100%=83%. =
=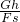 =
=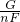 求出D完全提出水面后,滑轮组提升圆柱体B的机械效率.
求出D完全提出水面后,滑轮组提升圆柱体B的机械效率.

 考前必练系列答案
考前必练系列答案科目:初中物理 来源: 题型:
 (2013?昌平区二模)如图甲所示是一个装置示意图,正方体A作为配重使用,保证杠杆EOF始终在水平位置平衡.某同学用这个装置和一个圆柱形密闭容器D提取水中的圆柱体B;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率和密闭容器D匀速被提升的距离关系如图22乙所示;在提升全过程中,密闭容器D上升速度始终保持不变,配重A始终没有离开地面,每个滑轮的质量都相等.已知密闭容器D的底面积为SD=1.2×10-2m2,质量为mD=3kg;正方体A单独放在水平地面上,对地面的压强为p0=3×104Pa,密闭容器D未被提出水面匀速上升和完全提出水面后匀速上升,A对地面的压强分别为p1=2.1×104 Pa,p2=1.3×104 Pa.(不计绳的重力,滑轮与轴的摩擦及水的阻力,不考虑水面高度变化,g取10N/kg)
(2013?昌平区二模)如图甲所示是一个装置示意图,正方体A作为配重使用,保证杠杆EOF始终在水平位置平衡.某同学用这个装置和一个圆柱形密闭容器D提取水中的圆柱体B;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率和密闭容器D匀速被提升的距离关系如图22乙所示;在提升全过程中,密闭容器D上升速度始终保持不变,配重A始终没有离开地面,每个滑轮的质量都相等.已知密闭容器D的底面积为SD=1.2×10-2m2,质量为mD=3kg;正方体A单独放在水平地面上,对地面的压强为p0=3×104Pa,密闭容器D未被提出水面匀速上升和完全提出水面后匀速上升,A对地面的压强分别为p1=2.1×104 Pa,p2=1.3×104 Pa.(不计绳的重力,滑轮与轴的摩擦及水的阻力,不考虑水面高度变化,g取10N/kg)查看答案和解析>>
科目:初中物理 来源: 题型:
 小明是一个喜欢思考的学生,他想不同的物质吸热能力是否相同呢?于是他取沙子和水这两种不同物质,来探究它们吸热能力的差异.他设计如图甲所示的实验装置.已有实验器材有:两个酒精灯,两个金属盒,温度计…在完成每一个实验步骤时要考虑很多问题,下面是小明的实验步骤,请根据要求补充完成;
小明是一个喜欢思考的学生,他想不同的物质吸热能力是否相同呢?于是他取沙子和水这两种不同物质,来探究它们吸热能力的差异.他设计如图甲所示的实验装置.已有实验器材有:两个酒精灯,两个金属盒,温度计…在完成每一个实验步骤时要考虑很多问题,下面是小明的实验步骤,请根据要求补充完成; 查看答案和解析>>
科目:初中物理 来源: 题型:
 用一个动滑轮把重为40N的日常生活用品提到6m高的楼上,如图甲所示,此装置的机械效率为80%(绳子重和摩擦不计)
用一个动滑轮把重为40N的日常生活用品提到6m高的楼上,如图甲所示,此装置的机械效率为80%(绳子重和摩擦不计)查看答案和解析>>
科目:初中物理 来源:2013年北京市昌平区中考物理二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com