
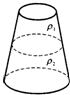
 如图所示,一只锥形烧瓶量得它的上口径与底径之比为1:3,放在水平桌面上,容器内有两种互不相溶的液体充满容器,且上、下两部分液体恰好深度相同.已知上、下两种液体的密度之比为ρ1:ρ2=1:2,设上部液体对下部液体的压力为F1,下部液体对瓶底的压力为F2,则F1:F2=4:27.
如图所示,一只锥形烧瓶量得它的上口径与底径之比为1:3,放在水平桌面上,容器内有两种互不相溶的液体充满容器,且上、下两部分液体恰好深度相同.已知上、下两种液体的密度之比为ρ1:ρ2=1:2,设上部液体对下部液体的压力为F1,下部液体对瓶底的压力为F2,则F1:F2=4:27. 分析 首先利用r=$\frac{{r}_{1}+{r}_{2}}{2}$求出锥形烧瓶的中间的口径与底径之比,然后根据S=πr2求出锥形烧瓶的中间面积与底面积之比,
再根据p=ρgh表示出上部液体对下部液体的压强和下部部液体对瓶底的压强的表达式,
最后根据F=pS表示出上部液体对下部液体的压力和下部液体对瓶底的压力的表达式,进而求出压力之比.
解答 解:锥形烧瓶的上口径与底径之比r1:r2=1:3,
则中间的口径r=$\frac{{r}_{1}+{r}_{2}}{2}$
故锥形烧瓶的中间的口径与底径之比:
r:r2=$\frac{{r}_{1}+{r}_{2}}{2}$:r2=$\frac{\frac{{r}_{2}}{3}+{r}_{2}}{2}$:r2=2:3,
由S=πr2得,锥形烧瓶的中间面积与底面积之比:
S:S2=πr2:π${r}_{2}^{2}$=r2:${r}_{2}^{2}$=4:9,
由p=ρgh得,上部液体对下部液体的压强:
p1=ρ1gh,
下部部液体对瓶底的压强:
p2=ρ1gh+ρ2gh,
由p=$\frac{F}{S}$得,上部液体对下部液体的压力:
F1=p1S=ρ1ghS,
下部液体对瓶底的压力:
F2=p2S=(ρ1gh+ρ2gh)S2,
则$\frac{{F}_{1}}{{F}_{2}}$=$\frac{{ρ}_{1}ghS}{({ρ}_{1}gh+{ρ}_{2}gh){S}_{2}}$=$\frac{{ρ}_{1}S}{({ρ}_{1}+{ρ}_{2}){S}_{2}}$=$\frac{1×4}{(1+2)×9}$=$\frac{4}{27}$,
即:F1:F2=4:27.
故答案为:4:27.
点评 本题考查了学生对压强公式及液体压强公式的掌握和应用,注意公式及变形公式的灵活运用,对于形状不规则的容器,先根据p=ρgh求压强,再利用F=pS求压力是正确解题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:选择题
| A. | 由R=$\frac{U}{I}$可知,导体电阻R与U成正比 | B. | 不管U如何变化,U和L的比值不变 | ||
| C. | U增加几倍,电流就增加几倍 | D. | 当U一定时,电流也不变 |
查看答案和解析>>
科目:初中物理 来源: 题型:选择题
| A. | 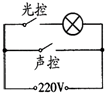 | B. |  | C. |  | D. | 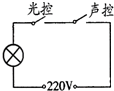 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com