
 如图,一重为G、密度为ρ的金属块A沉在水中的斜坡上,在沿斜坡向上的拉力F作用下,物块A以v的速度沿斜坡匀速上升,斜坡的倾角为θ,斜面效率为η,若不计水的阻力,求拉力F的功率和物块A受到的摩擦力?(水的密度为ρ0)
如图,一重为G、密度为ρ的金属块A沉在水中的斜坡上,在沿斜坡向上的拉力F作用下,物块A以v的速度沿斜坡匀速上升,斜坡的倾角为θ,斜面效率为η,若不计水的阻力,求拉力F的功率和物块A受到的摩擦力?(水的密度为ρ0) ,
,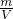 可得,金属块的体积:
可得,金属块的体积: =
=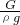 ,
,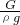 =
= ;
; )h=
)h= ,
,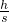 ,
,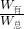 ×100%=
×100%= ×100%,
×100%, =
= ×
×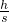 =
= sinθ,
sinθ, sinθ×v=
sinθ×v= ;
; ,
, =F-
=F- .
. ;物块A受到的摩擦力为F-
;物块A受到的摩擦力为F- .
.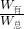 ×100%即可求出拉力F的,根据P=Fv即可求出拉力F的功率.
×100%即可求出拉力F的,根据P=Fv即可求出拉力F的功率.

科目:初中物理 来源: 题型:
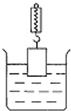 如图所示,有一重为G=27N的长方体物体,长L=20cm,它的横截面积S1,是盛水容器横截面积S2(容器壁厚不计)的1/3,当物体有2/5的体积浸入水中时,弹簧测力计的示数为F=23N(g取10N/kg)根据题中所给条件,试一试你能求出与物体有关的物理量有哪些?请分别用符号代入公式计算出结果.
如图所示,有一重为G=27N的长方体物体,长L=20cm,它的横截面积S1,是盛水容器横截面积S2(容器壁厚不计)的1/3,当物体有2/5的体积浸入水中时,弹簧测力计的示数为F=23N(g取10N/kg)根据题中所给条件,试一试你能求出与物体有关的物理量有哪些?请分别用符号代入公式计算出结果.查看答案和解析>>
科目:初中物理 来源: 题型:
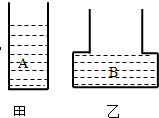 (2009?丰台区二模)如图所示,甲、乙两容器内装有A、B两种体积相同的液体,甲容器的底面积是乙容器底面积的一半,B刚好把乙容器下半部装满,乙容器开口部分的面积和底面积之比为
(2009?丰台区二模)如图所示,甲、乙两容器内装有A、B两种体积相同的液体,甲容器的底面积是乙容器底面积的一半,B刚好把乙容器下半部装满,乙容器开口部分的面积和底面积之比为| 2 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中物理 来源: 题型:
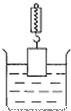
 如图,一重为G、密度为ρ的金属块A沉在水中的斜坡上,在沿斜坡向上的拉力F作用下,物块A以v的速度沿斜坡匀速上升,斜坡的倾角为θ,斜面效率为η,若不计水的阻力,求拉力F的功率和物块A受到的摩擦力?(水的密度为ρ0)
如图,一重为G、密度为ρ的金属块A沉在水中的斜坡上,在沿斜坡向上的拉力F作用下,物块A以v的速度沿斜坡匀速上升,斜坡的倾角为θ,斜面效率为η,若不计水的阻力,求拉力F的功率和物块A受到的摩擦力?(水的密度为ρ0)查看答案和解析>>
科目:初中物理 来源:2009-2010学年沪科版八年级(下)期中物理试卷(8)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com