
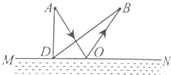
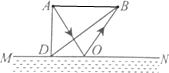
 (2013?安徽)如图,A、B两地相距4km,MN是与AB连线平行的一条小河的河岸,AB到河岸的垂直距离为3km,小军要从A处走到河岸取水然后送到B处,他先沿着垂直于河岸的方向到D点取水,再沿直线DB到B处.若小军的速度大小恒为5km/h,不考虑取水停留的时间.
(2013?安徽)如图,A、B两地相距4km,MN是与AB连线平行的一条小河的河岸,AB到河岸的垂直距离为3km,小军要从A处走到河岸取水然后送到B处,他先沿着垂直于河岸的方向到D点取水,再沿直线DB到B处.若小军的速度大小恒为5km/h,不考虑取水停留的时间.| s |
| t |
| s |
| t |
| s |
| v |
| 8km |
| 5km/h |


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中物理 来源: 题型:
 (2013?安徽)如图,静止在花朵上的是一种叫“全碳气凝胶”的固体材料,它是我国科学家研制的迄今为止世界上最轻的材料.一块体积为100cm3的“全碳气凝胶”的质量只有0.016g,则它的密度为
(2013?安徽)如图,静止在花朵上的是一种叫“全碳气凝胶”的固体材料,它是我国科学家研制的迄今为止世界上最轻的材料.一块体积为100cm3的“全碳气凝胶”的质量只有0.016g,则它的密度为查看答案和解析>>
科目:初中物理 来源: 题型:
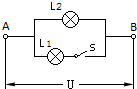 (2013?安徽)如图,小灯泡L1与L2均标有“1.5V,0.3A”字样,AB两端的电压U=1.5V.开关S断开时,通过L2的电流为
(2013?安徽)如图,小灯泡L1与L2均标有“1.5V,0.3A”字样,AB两端的电压U=1.5V.开关S断开时,通过L2的电流为查看答案和解析>>
科目:初中物理 来源: 题型:
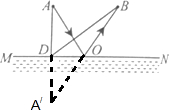
 (2013?安徽)如图,轻质杠杆AB可以绕O点转动,在A点用细线悬挂一重物,在B点施加一个竖直向下的动力,使核杠杆在水平位置保持平衡.若将动力的方向改为沿虚线方向,仍使杠杆在水平位置平衡,则( )
(2013?安徽)如图,轻质杠杆AB可以绕O点转动,在A点用细线悬挂一重物,在B点施加一个竖直向下的动力,使核杠杆在水平位置保持平衡.若将动力的方向改为沿虚线方向,仍使杠杆在水平位置平衡,则( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com