
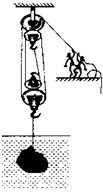
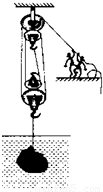
 产自我市的岩滩红水河奇石闻名全国乃至世界,采石工人用如图所示的装置将一块奇石从5m深的水底提升到离水面1m高的船上.已知石头在出水前人的拉力F1=4.5×103N,石头出水后人的拉力F2=7.0×103N,不计摩擦及动滑轮重,g取10N/kg,求:
产自我市的岩滩红水河奇石闻名全国乃至世界,采石工人用如图所示的装置将一块奇石从5m深的水底提升到离水面1m高的船上.已知石头在出水前人的拉力F1=4.5×103N,石头出水后人的拉力F2=7.0×103N,不计摩擦及动滑轮重,g取10N/kg,求: G石,
G石, (G石-F浮)
(G石-F浮)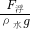 =
=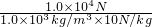 =1m3,
=1m3, G石求拉力大小;
G石求拉力大小; F拉=
F拉= (G石-F浮)求石头的浮力,再根据阿基米德原理求排开水的体积(石头的体积);
(G石-F浮)求石头的浮力,再根据阿基米德原理求排开水的体积(石头的体积); G这个关系.
G这个关系. 

科目:初中物理 来源: 题型:
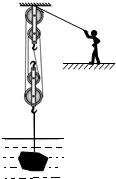 (2005?河池)产自我市的岩滩红水河奇石闻名全国乃至世界,采石工人用如图所示的装置将一块奇石从5m深的水底提升到离水面1m高的船上.已知石头在出水前人的拉力F1=4.5×103N,石头出水后人的拉力F2=7.0×103N,不计摩擦及动滑轮重,g取10N/kg,求:
(2005?河池)产自我市的岩滩红水河奇石闻名全国乃至世界,采石工人用如图所示的装置将一块奇石从5m深的水底提升到离水面1m高的船上.已知石头在出水前人的拉力F1=4.5×103N,石头出水后人的拉力F2=7.0×103N,不计摩擦及动滑轮重,g取10N/kg,求:查看答案和解析>>
科目:初中物理 来源:2005年广西河池市中考物理试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com