

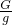 =
=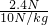 =0.24kg,
=0.24kg, =
=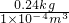 =2.4×103kg/m3.
=2.4×103kg/m3.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中物理 来源: 题型:
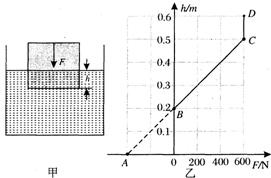 为了给立方体工件表面均匀地涂上某种油,需要用竖直向下的力F把漂浮在油面上的工件缓缓地压入油内,如图甲所示.工件的下底面与油面的距离为h,力F与h的大小关系如图乙所示.小科觉得图中CB的延长线BA段是没有意义的,老师告诉他,力F为负值时,表明它的方向与原来的方向相反了.
为了给立方体工件表面均匀地涂上某种油,需要用竖直向下的力F把漂浮在油面上的工件缓缓地压入油内,如图甲所示.工件的下底面与油面的距离为h,力F与h的大小关系如图乙所示.小科觉得图中CB的延长线BA段是没有意义的,老师告诉他,力F为负值时,表明它的方向与原来的方向相反了.查看答案和解析>>
科目:初中物理 来源: 题型:
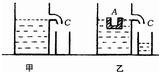 (2002?苏州)如图甲所示,一圆柱形容器竖直放置在水平桌面上,其侧壁有一溢水口C,容器内的液面恰好与溢水口C齐平.先将一个由均匀材料制成的船形物A开口向上放入容器中,当船形物漂浮.在液面上(如图乙所示),从溢水口溢出液体的体积为V;然后使船形物A反转90°,当它浸没在液体中后容器内的液面下降了h(在船形物由漂浮到浸没的过程器内的液体未溢出).已知圆柱形容器的底面积为S,液体的密度为ρ,
(2002?苏州)如图甲所示,一圆柱形容器竖直放置在水平桌面上,其侧壁有一溢水口C,容器内的液面恰好与溢水口C齐平.先将一个由均匀材料制成的船形物A开口向上放入容器中,当船形物漂浮.在液面上(如图乙所示),从溢水口溢出液体的体积为V;然后使船形物A反转90°,当它浸没在液体中后容器内的液面下降了h(在船形物由漂浮到浸没的过程器内的液体未溢出).已知圆柱形容器的底面积为S,液体的密度为ρ,| ρV |
| V-Sh |
| ρV |
| V-Sh |
查看答案和解析>>
科目:初中物理 来源: 题型:
 在一个足够深的容器内装有深4cm的水,将一个长10cm、横截面积50cm2的圆柱形实心塑料块挂于弹簧测力计上,当塑料块底面刚好接触水面时,弹簧测力计示数为4N,如图甲所示.已知弹簧的伸长量与受到的拉力成正比,弹簧受到1N的拉力时伸长1cm.若往容器内缓慢加水,此过程中水面升高的高度△H与所加水的体积V的关系如图乙所示.
在一个足够深的容器内装有深4cm的水,将一个长10cm、横截面积50cm2的圆柱形实心塑料块挂于弹簧测力计上,当塑料块底面刚好接触水面时,弹簧测力计示数为4N,如图甲所示.已知弹簧的伸长量与受到的拉力成正比,弹簧受到1N的拉力时伸长1cm.若往容器内缓慢加水,此过程中水面升高的高度△H与所加水的体积V的关系如图乙所示.查看答案和解析>>
科目:初中物理 来源: 题型:
 (2012?潍坊)小丽要研究金属圆柱体受的浮力与浸没在水中深度h的关系,实验装置如图甲所示,在弹簧测力计下挂一个金属圆柱体,测出金属圆柱体的重力,然后让圆柱体缓慢地浸入水中,从圆柱体底面接触水面开始,到完全浸没水中(未接触容器底部),记录圆柱体浸入水中不同深度h时测力计的示数,并得到测力计示数F1和圆柱体受的浮力F2随h变化的图象,图中能反映圆柱体受的浮力F2随h变化的图象是
(2012?潍坊)小丽要研究金属圆柱体受的浮力与浸没在水中深度h的关系,实验装置如图甲所示,在弹簧测力计下挂一个金属圆柱体,测出金属圆柱体的重力,然后让圆柱体缓慢地浸入水中,从圆柱体底面接触水面开始,到完全浸没水中(未接触容器底部),记录圆柱体浸入水中不同深度h时测力计的示数,并得到测力计示数F1和圆柱体受的浮力F2随h变化的图象,图中能反映圆柱体受的浮力F2随h变化的图象是查看答案和解析>>
科目:初中物理 来源: 题型:
 下面是同学们做过的一些物理实验情景图,请你对这些实验现象分别进行分析并得出结论:
下面是同学们做过的一些物理实验情景图,请你对这些实验现象分别进行分析并得出结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com