
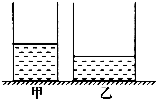
 如图所示,水平地面上的轻质圆柱形容器甲、乙分别盛有质量均为m的水和酒精,甲、乙的底面积分别为S,2S.(ρ酒精=0.8×103千克/米3);
如图所示,水平地面上的轻质圆柱形容器甲、乙分别盛有质量均为m的水和酒精,甲、乙的底面积分别为S,2S.(ρ酒精=0.8×103千克/米3);| 物体 | 密度 | 体积 |
| A | ρ | 2V |
| B | 3ρ | V |
 得:
得: =
= =2×10-3m3;
=2×10-3m3; 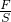 可知:要使压强最大,则容器的底面积为最小,
可知:要使压强最大,则容器的底面积为最小, =
= .
. .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中物理 来源: 题型:
 如图所示,水平地面上的物体,在水平恒定的拉力F的作用下,沿ABC方向做直线运动,已知AB=BC,设AB段是光滑的,拉力F做功为W1,BC段是粗糙的,拉力F做功为W2,则W1和W2的关系是( )
如图所示,水平地面上的物体,在水平恒定的拉力F的作用下,沿ABC方向做直线运动,已知AB=BC,设AB段是光滑的,拉力F做功为W1,BC段是粗糙的,拉力F做功为W2,则W1和W2的关系是( )查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,水平地面上甲乙两圆柱形容器中的液面相平,A、B、C三点液体的压强分别为PA、PB和PC,则PA、PB和PC的大小关系是
如图所示,水平地面上甲乙两圆柱形容器中的液面相平,A、B、C三点液体的压强分别为PA、PB和PC,则PA、PB和PC的大小关系是查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,水平地面上甲、乙两圆柱形容器中的液面相平,A、B、C三点液体的压强分别为 pA、pB和pC.(ρ酒精=0.8×103 kg/m3)
如图所示,水平地面上甲、乙两圆柱形容器中的液面相平,A、B、C三点液体的压强分别为 pA、pB和pC.(ρ酒精=0.8×103 kg/m3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com