
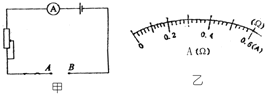
 科技小组自制一台可以测量电阻阻值的电阻表,如图所示,电阻表是由一只量程为“0~0.6A”的电流表和一个滑动变阻器和干电池(设电压不变)组成.使用时,把待测电阻接在A、B两端,为了直接从电流表的表盘上读出A、B端接入的电阻的阻值,需要在表盘上重新标示A、B间所测电阻的阻值数,当将A、B两端用直导线连接在一起时,调节滑动变阻器使电流表的指针偏转到最大位置(满偏),电源电压为1.5V,并保持不变.
科技小组自制一台可以测量电阻阻值的电阻表,如图所示,电阻表是由一只量程为“0~0.6A”的电流表和一个滑动变阻器和干电池(设电压不变)组成.使用时,把待测电阻接在A、B两端,为了直接从电流表的表盘上读出A、B端接入的电阻的阻值,需要在表盘上重新标示A、B间所测电阻的阻值数,当将A、B两端用直导线连接在一起时,调节滑动变阻器使电流表的指针偏转到最大位置(满偏),电源电压为1.5V,并保持不变.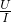 =
= =2.5Ω.
=2.5Ω. =
=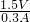 =5Ω,
=5Ω, =
=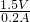 =7.5Ω,
=7.5Ω,
 ,可见I与Rx不成正比,
,可见I与Rx不成正比,

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中物理 来源: 题型:
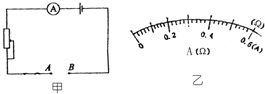 科技小组自制一台可以测量电阻阻值的电阻表,如图所示,电阻表是由一只量程为“0~0.6A”的电流表和一个滑动变阻器和干电池(设电压不变)组成.使用时,把待测电阻接在A、B两端,为了直接从电流表的表盘上读出A、B端接入的电阻的阻值,需要在表盘上重新标示A、B间所测电阻的阻值数,当将A、B两端用直导线连接在一起时,调节滑动变阻器使电流表的指针偏转到最大位置(满偏),电源电压为1.5V,并保持不变.
科技小组自制一台可以测量电阻阻值的电阻表,如图所示,电阻表是由一只量程为“0~0.6A”的电流表和一个滑动变阻器和干电池(设电压不变)组成.使用时,把待测电阻接在A、B两端,为了直接从电流表的表盘上读出A、B端接入的电阻的阻值,需要在表盘上重新标示A、B间所测电阻的阻值数,当将A、B两端用直导线连接在一起时,调节滑动变阻器使电流表的指针偏转到最大位置(满偏),电源电压为1.5V,并保持不变.查看答案和解析>>
科目:初中物理 来源: 题型:
 (2003?天津)某校科技小组自制一台可以测量电阻阻值的欧姆表,如图所示,欧姆表电路由一只灵敏电流表 G,定值电阻 R0,滑动变阻器和干电池(设 电压不变)组成.使用时可把待测电阻接在 A、B 两端.为了能直接从灵敏电流 表表盘上读出 A、B 端接入的电阻的阻值,需在表盘上重新标注 A、B 间所测的 电阻的阻值数.当将 A、B 两端直接连接在一起时,调节滑动变阻器使灵敏电流 表指针偏转到最大位置处(满偏),已知此时灵敏电流表内阻、滑动变阻器的 有效值和定值电阻 R0 的总阻值为 15Ω.问:
(2003?天津)某校科技小组自制一台可以测量电阻阻值的欧姆表,如图所示,欧姆表电路由一只灵敏电流表 G,定值电阻 R0,滑动变阻器和干电池(设 电压不变)组成.使用时可把待测电阻接在 A、B 两端.为了能直接从灵敏电流 表表盘上读出 A、B 端接入的电阻的阻值,需在表盘上重新标注 A、B 间所测的 电阻的阻值数.当将 A、B 两端直接连接在一起时,调节滑动变阻器使灵敏电流 表指针偏转到最大位置处(满偏),已知此时灵敏电流表内阻、滑动变阻器的 有效值和定值电阻 R0 的总阻值为 15Ω.问:查看答案和解析>>
科目:初中物理 来源:《14.2 欧姆定律》2013年同步练习(四)(解析版) 题型:解答题
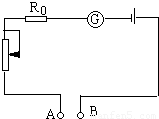 某校科技小组自制一台可以测量电阻阻值的欧姆表,如图所示,欧姆表电路由一只灵敏电流表 G,定值电阻 R,滑动变阻器和干电池(设 电压不变)组成.使用时可把待测电阻接在 A、B 两端.为了能直接从灵敏电流 表表盘上读出 A、B 端接入的电阻的阻值,需在表盘上重新标注 A、B 间所测的 电阻的阻值数.当将 A、B 两端直接连接在一起时,调节滑动变阻器使灵敏电流 表指针偏转到最大位置处(满偏),已知此时灵敏电流表内阻、滑动变阻器的 有效值和定值电阻 R 的总阻值为 15Ω.问:
某校科技小组自制一台可以测量电阻阻值的欧姆表,如图所示,欧姆表电路由一只灵敏电流表 G,定值电阻 R,滑动变阻器和干电池(设 电压不变)组成.使用时可把待测电阻接在 A、B 两端.为了能直接从灵敏电流 表表盘上读出 A、B 端接入的电阻的阻值,需在表盘上重新标注 A、B 间所测的 电阻的阻值数.当将 A、B 两端直接连接在一起时,调节滑动变阻器使灵敏电流 表指针偏转到最大位置处(满偏),已知此时灵敏电流表内阻、滑动变阻器的 有效值和定值电阻 R 的总阻值为 15Ω.问:查看答案和解析>>
科目:初中物理 来源:2011年湖北省武汉市黄陂一中分配生素质测试(解析版) 题型:解答题
查看答案和解析>>
科目:初中物理 来源:2003年天津市中考物理试卷(解析版) 题型:解答题
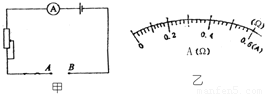
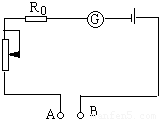 某校科技小组自制一台可以测量电阻阻值的欧姆表,如图所示,欧姆表电路由一只灵敏电流表 G,定值电阻 R,滑动变阻器和干电池(设 电压不变)组成.使用时可把待测电阻接在 A、B 两端.为了能直接从灵敏电流 表表盘上读出 A、B 端接入的电阻的阻值,需在表盘上重新标注 A、B 间所测的 电阻的阻值数.当将 A、B 两端直接连接在一起时,调节滑动变阻器使灵敏电流 表指针偏转到最大位置处(满偏),已知此时灵敏电流表内阻、滑动变阻器的 有效值和定值电阻 R 的总阻值为 15Ω.问:
某校科技小组自制一台可以测量电阻阻值的欧姆表,如图所示,欧姆表电路由一只灵敏电流表 G,定值电阻 R,滑动变阻器和干电池(设 电压不变)组成.使用时可把待测电阻接在 A、B 两端.为了能直接从灵敏电流 表表盘上读出 A、B 端接入的电阻的阻值,需在表盘上重新标注 A、B 间所测的 电阻的阻值数.当将 A、B 两端直接连接在一起时,调节滑动变阻器使灵敏电流 表指针偏转到最大位置处(满偏),已知此时灵敏电流表内阻、滑动变阻器的 有效值和定值电阻 R 的总阻值为 15Ω.问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com