
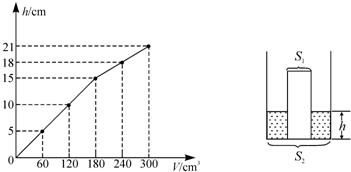
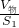 =
=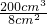 =25cm;
=25cm;

科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,一圆柱形平底容器底面积为4×10-2m2,把它放在水平桌面上,在容器内放入一个底面积为2×10-2m2,重为20N的圆柱形物块,物块的密度为0.8×103Kg/m3.则物块对容器底的压强等于
如图所示,一圆柱形平底容器底面积为4×10-2m2,把它放在水平桌面上,在容器内放入一个底面积为2×10-2m2,重为20N的圆柱形物块,物块的密度为0.8×103Kg/m3.则物块对容器底的压强等于查看答案和解析>>
科目:初中物理 来源:2013-2014学年上海市普陀区初三上学期期末测试物理试卷(解析版) 题型:计算题
在一底面积为1.5×10−2米2的圆柱形容器内放入一个密度均匀的质量为0.6千克、底面积为1×10−2米2、高度为0.08米的柱状木块,然后向容器内注入一定量的水使木块漂浮在水面上,如图12所示,此时水面高度为0.1米。

① 求水对容器底部的压强p水。
② 求木块浸入水体积与木块体积之比V浸∶V木。
③ 若将木块沿虚线以下截取整个木块的一半后,求木块上表面下降的高度h。
查看答案和解析>>
科目:初中物理 来源:2013年湖北省武汉市部分学校五月调考物理试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com