

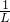 的图象如图乙,由图象可得出杠杆平衡的条件是F与L成______比.根据杠杆平衡条件,当F=2N时,可求出重力G的力臂是______m.
的图象如图乙,由图象可得出杠杆平衡的条件是F与L成______比.根据杠杆平衡条件,当F=2N时,可求出重力G的力臂是______m.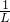 成正比,
成正比, 为定值,所以FL为定值,可以推断F-L成反比.
为定值,所以FL为定值,可以推断F-L成反比.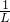 =4m-1,所以L=0.25m,
=4m-1,所以L=0.25m,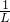 的图线知,F和
的图线知,F和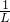 成正比,可以推断F-L成反比.
成正比,可以推断F-L成反比.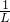 的图线如图乙,当F=2N,
的图线如图乙,当F=2N,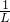 =4m-1时,杠杆处于平衡状态,根据
=4m-1时,杠杆处于平衡状态,根据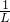 =4m-1求出F的力臂L,根据杠杆平衡条件求出重力G的力臂.
=4m-1求出F的力臂L,根据杠杆平衡条件求出重力G的力臂.

 科学实验活动册系列答案
科学实验活动册系列答案科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:

| 1 | L |
查看答案和解析>>
科目:初中物理 来源: 题型:

| 1 | L |
查看答案和解析>>
科目:初中物理 来源: 题型:

查看答案和解析>>
科目:初中物理 来源: 题型:
 某同学用如图甲所示的弹簧测力计测某物体的重力,此时弹簧测力计的指针指示情况如图乙所示,他据此读出该物体的重力为3.2.你认为他在测量中错误的地方是:
某同学用如图甲所示的弹簧测力计测某物体的重力,此时弹簧测力计的指针指示情况如图乙所示,他据此读出该物体的重力为3.2.你认为他在测量中错误的地方是:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com