
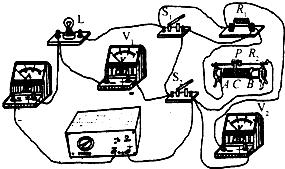
 如图所示的电路中,电源两端电压保持不变.当开关S1、S2都闭合时,灯L正常发光,电流表的示数为I1灯L的电功率为PL;当开关S1、S2都断开时,滑动变阻器接入电路的电阻为RC,电流表的示数为I2,灯L的电功率为PL′,电压表V1的示数为U1,电压表V2的示数为U2,且U1:U2=3:2,PL:PL′=4:1.当通过闭合或断开开关及移动滑动变阻器的滑片P时,会形成不同的电路,在这些不同的电路中,电路消耗的最大功率与电路消耗的最小功率之比为3:1,电路消耗的功率最小时滑动变阻器的电功率为3W(忽略温度对灯丝电阻的影响).求:
如图所示的电路中,电源两端电压保持不变.当开关S1、S2都闭合时,灯L正常发光,电流表的示数为I1灯L的电功率为PL;当开关S1、S2都断开时,滑动变阻器接入电路的电阻为RC,电流表的示数为I2,灯L的电功率为PL′,电压表V1的示数为U1,电压表V2的示数为U2,且U1:U2=3:2,PL:PL′=4:1.当通过闭合或断开开关及移动滑动变阻器的滑片P时,会形成不同的电路,在这些不同的电路中,电路消耗的最大功率与电路消耗的最小功率之比为3:1,电路消耗的功率最小时滑动变阻器的电功率为3W(忽略温度对灯丝电阻的影响).求: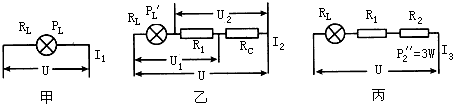
 =
=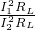 =(
=(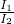 )2=
)2=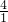 ,
,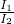 =
= ;
;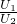 =
=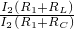 =
=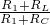 =
= ,
,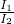 =
=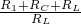 =
= ,
, ,
,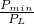 =
=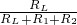 =
= ,
, =
= ;
;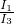 =
=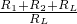 =
=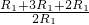 =
= ,
, R2=6P2″=6×3W=18W;
R2=6P2″=6×3W=18W;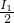 )2×(
)2×(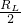 +RL+
+RL+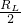 )=
)= ×I12RL=
×I12RL= ×18W=9W.
×18W=9W. 表示出电路中的最大和最小电功率结合阻值关系即可求出滑动变阻器的最大阻值R2与电阻R1的比值;
表示出电路中的最大和最小电功率结合阻值关系即可求出滑动变阻器的最大阻值R2与电阻R1的比值;

 名校课堂系列答案
名校课堂系列答案科目:初中物理 来源: 题型:


查看答案和解析>>
科目:初中物理 来源: 题型:
 (2013?顺义区一模)在如图所示的电路中,电源两端电压不变.当只闭合开关S1且滑动变阻器R3接入电路电阻值最大时,电压表的示数为3.6V,滑动变阻器消耗的电功率为1.44W,电阻R1消耗的电功率为P1.当只闭合开关S2且滑动变阻器R3的滑片P在中点时,电压表示数为4.5V,电阻R2消耗的电功率为P2.若P1:P2=8:15,则电阻R2在1min40s内所消耗的电能为
(2013?顺义区一模)在如图所示的电路中,电源两端电压不变.当只闭合开关S1且滑动变阻器R3接入电路电阻值最大时,电压表的示数为3.6V,滑动变阻器消耗的电功率为1.44W,电阻R1消耗的电功率为P1.当只闭合开关S2且滑动变阻器R3的滑片P在中点时,电压表示数为4.5V,电阻R2消耗的电功率为P2.若P1:P2=8:15,则电阻R2在1min40s内所消耗的电能为查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示的电路中,电源电压为12伏,S断开时,A2表的示数为0.3安;S闭合时,A2表的示数为0.4安,这时A1表的示数为
如图所示的电路中,电源电压为12伏,S断开时,A2表的示数为0.3安;S闭合时,A2表的示数为0.4安,这时A1表的示数为查看答案和解析>>
科目:初中物理 来源:2013年山东省临沂市高级中等学校招生考试物理 题型:013
如图所示的电路中.电饭电压保持不变,闭合开关S后

A.电压表的示数变大
B.电流表的示数变大
C.电路中的总电阻变大
D.电路消耗的总功率变小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com