（2008?浦东新区二模）某研究性学习小组的同学为了制作能够方便鉴别液体种类的仪器，他们猜测漂浮在液面上的物体浸在液体中的深度可能与物体的质量、液体的种类存在着某种关系．实验时，该小组同学选用一个圆柱形的瓶子，内装不同质量的细沙，先后漂浮在甲、乙和丙三种液体中（已知ρ
甲＜ρ
乙＜ρ
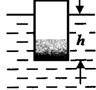
丙），并用仪器测出每一次实验时瓶和细沙的总质量及圆柱形的瓶子底部所处的深度h，如图所示．记录的数据如表一、表二与表三所示．
| 表一 液体甲 |
|
表二 液体乙 |
|
表三 液体丙 |
实验
序号 |
瓶和沙质量
（千克） |
深度
（米） |
|
实验
序号 |
瓶和沙质量
（千克） |
深度
（米） |
|
实验
序号 |
瓶和沙质量
（千克） |
深度
（米） |
| 1 |
0.2 |
0.18 |
|
4 |
0.2 |
0.15 |
|
7 |
0.2 |
0.13 |
| 2 |
0.4 |
0.36 |
|
5 |
0.4 |
0.30 |
|
8 |
0.4 |
0.26 |
| 3 |
0.6 |
0.54 |
|
6 |
0.6 |
0.45 |
|
9 |
0.6 |
0.39 |
（1）分析比较实验序号
1、2与3或4、5与6（或7、8与9）
1、2与3或4、5与6（或7、8与9）
的数据及相关条件，可初步得出结论：漂浮在同种液体中的不同圆柱体，它浸在液体中的深度与它的质量成正比．
（2）分析比较实验序号1、4与7或2、5与8（或3、6与9）的数据及相关条件，可初步得出结论：
漂浮在不同液体中的同一圆柱体，液体的密度越小，圆柱体浸在液体中的深度越大
漂浮在不同液体中的同一圆柱体，液体的密度越小，圆柱体浸在液体中的深度越大
．
（3）该小组同学得出了以上的结论后，又对表中的实验数据进行进一步综合运算和分析，发现了新的规律：
A、分析表一或表二或表三中的数据及相关条件可知：当圆柱体漂浮在
同种液面上的圆柱体的质量与物体浸在液体中的深度的比值相同
同种液面上的圆柱体的质量与物体浸在液体中的深度的比值相同
．
B、分析表一和表二和表三中的数据及相关条件可知：当圆柱体漂浮在
不同液面上的圆柱体的质量与物体浸在液体中的深度的比值不同，且液体的密度越大，比值也越大
不同液面上的圆柱体的质量与物体浸在液体中的深度的比值不同，且液体的密度越大，比值也越大
．
已知甲、乙、丙的质量分别为1kg、2kg、3kg，三个正方体的一个面的面积分别是10cm2、20cm2和30cm2，如图所示放在水平地面上，设甲对乙的压强为p1，乙対丙的压强为p2，丙对地面的压强为p3，则（ ）
已知甲、乙、丙的质量分别为1kg、2kg、3kg，三个正方体的一个面的面积分别是10cm2、20cm2和30cm2，如图所示放在水平地面上，设甲对乙的压强为p1，乙対丙的压强为p2，丙对地面的压强为p3，则
