
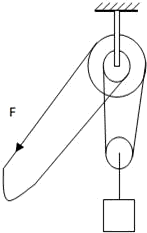
 工厂里有一种特殊结构的滑轮,叫做差动滑轮(俗称神仙葫芦),它由两个直径相差不多的定滑轮和一个动滑轮组成,其示意图如图所示.有了它,只需一个人就可以缓缓吊起或移动很重的物体.你能分析一下其中的道理吗?
工厂里有一种特殊结构的滑轮,叫做差动滑轮(俗称神仙葫芦),它由两个直径相差不多的定滑轮和一个动滑轮组成,其示意图如图所示.有了它,只需一个人就可以缓缓吊起或移动很重的物体.你能分析一下其中的道理吗? 解:这种装置中两个连在一起的定滑轮同轴转动,绳在滑轮上不滑动,若设拉力为F,重物重为G,大定滑轮半径为R,小定滑轮半径为r,则F′=
解:这种装置中两个连在一起的定滑轮同轴转动,绳在滑轮上不滑动,若设拉力为F,重物重为G,大定滑轮半径为R,小定滑轮半径为r,则F′= ,FR=F′r,可知,F<F′<G,故有了这种装置,只需一个人就可以缓缓吊起或移动很重的物体;
,FR=F′r,可知,F<F′<G,故有了这种装置,只需一个人就可以缓缓吊起或移动很重的物体;  ×2π(R-r)=π(R-r),因此根据机械效率得:η=
×2π(R-r)=π(R-r),因此根据机械效率得:η= =
=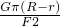 ,则:F=
,则:F=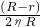 G.若将R做的较大,并使r与R相差很小,即轮与轴的半径很接近,则可用很小的拉力吊起很重的物体,达到省力效果.
G.若将R做的较大,并使r与R相差很小,即轮与轴的半径很接近,则可用很小的拉力吊起很重的物体,达到省力效果.

科目:初中物理 来源: 题型:
 工厂里有一种特殊结构的滑轮,叫做差动滑轮(俗称神仙葫芦),它由两个直径相差不多的定滑轮和一个动滑轮组成,其示意图如图所示.有了它,只需一个人就可以缓缓吊起或移动很重的物体.你能分析一下其中的道理吗?
工厂里有一种特殊结构的滑轮,叫做差动滑轮(俗称神仙葫芦),它由两个直径相差不多的定滑轮和一个动滑轮组成,其示意图如图所示.有了它,只需一个人就可以缓缓吊起或移动很重的物体.你能分析一下其中的道理吗?查看答案和解析>>
科目:初中物理 来源:《11.2 滑轮》2011年同步练习(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com