在一次爆破中,用一根长1m的导火线引爆炸药,导火线以0.5cm/s的速度燃烧,点火者点着导火线后以4m/s的速度跑开,他能否在爆炸前跑到离爆炸地点600m的安全地区?(通过列式计算来说明)
【答案】
分析:(1)方法一:已知导火线的长度和燃烧速度,可以得到导火线燃烧所用时间;已知点火者奔跑的速度和安全距离,可以得到点火者跑到安全区所用时间.将导火线燃烧完需要的时间和点火者跑到安全区所用时间相比较就能得到答案.
(2)方法二、已知导火线的长度和燃烧速度,可以得到导火线燃烧所用时间;此时间也就是点燃者快跑的时间,已知点火者奔跑的时间和速度,可以得到跑出的距离,将此距离与安全距离相比较就能得到答案.
(3)方法三、已知点火者奔跑的速度和安全距离,可以得到点火者到达安全区的时间;已知点火者到达安全区的时间和导火线燃烧的速度,可以得到点火者到达安全区导火线燃烧的长度.点火者到达安全区导火线燃烧的长度与导火线的总长度相比较也能得到答案.
解答:解:方法一:导火线燃烧完所用时间:
t
1=
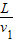
=
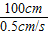
=200s,
人跑到安全地区需用的时间:
t
2=
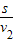
=
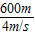
=150s,
因为 t
2<t
1,
所以能跑到安全区.
方法二:t
1=
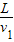
=
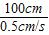
=200s,
人在t
1内能通过的路程s
2=v
2t
1=4m/s×200s=800m>600m,
所以能跑到安全区.
方法三:人跑到安全地区所需时间:
t
2=
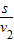
=
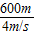
=150s,
经150s导火线燃烧的长度:
L=0.5cm/s×150s=75cm<100cm,
在导火线烧完前人能到安全地区.
答:导火线燃烧完之前人能到达安全区.
点评:本题属于方法开放性习题,解法有多种,但基本思路一致:确定两个物体运动过程中的不变量,据此相互联系,找出等量关系式进行求解.

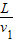 =
=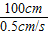 =200s,
=200s,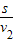 =
=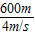 =150s,
=150s,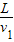 =
=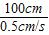 =200s,
=200s,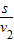 =
=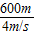 =150s,
=150s,
